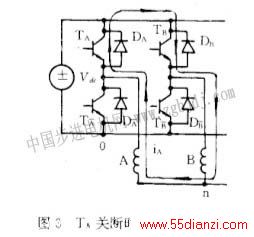
b．TA关断时ia的正向回路。A绕组内的正向电流，经其他反向导通的相绕组及相应的功放管，再经过Dx回到A相绕组的端点形成闭合回路，如图2所示。
c．Tx丙导通时ia的反向回路。电源正端经其他正向导通的功放管及相绕组，至A相绕组，再通过Tx到电源负端。
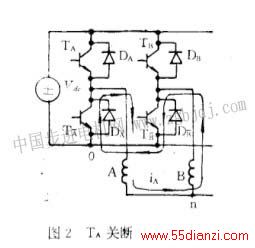d．Tx不导通时ia的反向回路。A绕组内的反向电流，经过DA至其他正向导通的功放管及相应的绕组形成闭合回路，如图3所示。
可见，对于任一相绕组，不论其相应桥臂的功放管导通与不导通，都可形成其正向电流或反向电流的回路。实际上，功放管只起到控制外加功放级电压的作用，使他能正向、反向或不加到相应相的绕组上去。对于任一相绕组，其电压方程式为：
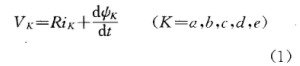
式中VK--K相绕组的外加电压，主要与功放管的导通情况有关，是不连续函数
R-相绕组回路的电阻
iK一一相绕组的电流
ψK相绕组的总磁链
LjK时为K相绕组的自感
j≠K时为K相与j相绕组间的互感
UθK——K相绕组的旋转感应电压
从迭加的概念出发，式(2)可改写为：
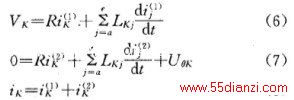相应地，电磁转矩也可分为2个分量，即
式中T(1)对应于iK(1)（K=a、b、c、d、e），若忽略旋转感应电压对绕组电流波形的影响，则分析或计算所得的电流和相应的电磁转矩就是该分量，他是电磁转矩中的基本分量。T(2)对应于iK
(2) (K=a、b、c、d、e)，这是对应于旋转感应电压的电流分量，由式(7)决定。从普通同步电机的理论和概念出发，就知道该转矩分量的值随转速变化的规律，他是制动转矩，相当于内部电磁阻尼[1]。
3短路转矩
转矩分量T(2)由电流分量iK
(2)决定，iK
(2)则可由式(7)解出。式(7)实际上是电机定子绕组短路运行的方程组。为简化起见，短路运行分析在下列假定条件下进行：①电机在恒转速下运行，ω=const。②旋转感应电压为正弦波形。③相绕组的自感及互感为常数。这是一种对称稳态运行，可写出其相量方程，且写出一相代表即可，例如写出A相的方程为：
由电动机结构的对称性可知：
由相电流的对称件（如图4所示）可得：
将式(11)～(13)代入式(10)，得相绕组电压平衡方程式的一般表达式：
式中Ls-相绕组的等效电感
I——相电流有效值
Uo——相绕组旋转感应电压有效值
由式(14)，短路电流为：
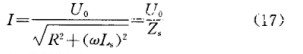短路转矩为：
从另一个角度出发，电机的电磁转矩也可以根据绕组电流及转矩系数求出，任一相绕组电流产生的电磁转矩为：
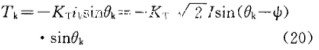总的电磁转矩：
实际上转矩系数KT与旋转感应电压系数Kt相等，所以时（18）与式(21)是完全一致的。
4试验校核
被试电机是一台90BYG550A型五相混合式步进电动机，其一相绕组通电时保持转矩测试结果如图5所示。
从曲线上对应额定相电流（J一3A）点得保持转矩为TK=0.6lNm，其转矩系数为：
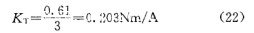
本文关键字：电动机 驱动电路及控制电路，单元电路 - 驱动电路及控制电路
上一篇：步进电动机驱动系统的单片机控制
