首先建立速度误差E、速度误差变化率EC和输出U的赋值表。
E={NL,NB,NM,NS,0,PS,PM,PB,PL};
EC={NL,NB,NM,NS,0,PS,PM,PB,PL};
U={NL,NB,NM,NS,0,PS,PM,PB,PL};
依据实际工作情况和操作经验,选取各输入量与输出量的论域:
E的模糊论域取[-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6];
EC的模糊论域取[-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6];
U的模糊论域取[-6,-5,-4,-3,-2,-1,0,+1,+2,+3,+4,+5,+6]。
隶属度函数的形状有很多种,由于人们对事物的判断往往沿用正态分布的思维特点,所以采用正态分布的隶属函数,即把三个模糊变量速度误差E、速度误差变化率EC和输出U看成是正态分布的,那么它们三个模糊子集的赋值表可用正态分布的隶属函数![]()
得到。通过计算可以得到速度误差E、速度误差变化率EC和输出U的赋值表。
4.3 系统软件构成
1、主程序的设计
本系统的主程序框图如图3所示。图中按照控制工艺要求给电机传送给定。当中断时间到达时,即进行参数自调整的模糊控制。参数自调整的模糊控制的框图如图4所示。
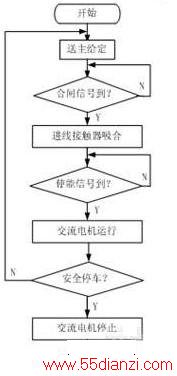
图3 主程序框图
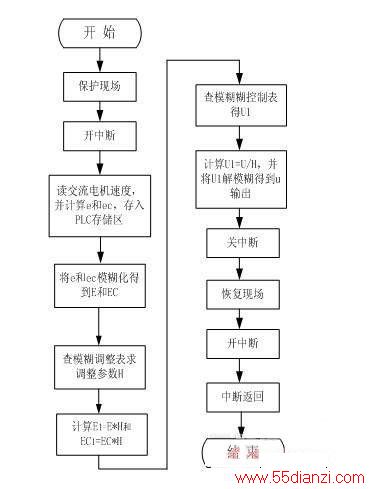
图4 参数自调整的模糊控制框图
5 仿真研究
在Matlab/Simulink仿真环境下,根据前面的设计,采用永磁同步电动机模型构建多电机同步控制系统仿真框图。图5为采用模糊控制补偿器的情况下三电动机速度响应曲线图。
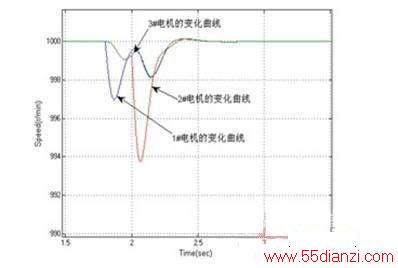
图5 电动机速度响应曲线
由仿真结果比较可以看出:采用模糊控制器的补偿方法时候,系统的同步性能、抗干扰性能力强,因而适合同步精度要求较高的场合。