0 引 言
短波 通信 是利用地波或低电离层进行几十千米到几百千米的中、近距离通信，利用电离层反射进行数千乃至上万千米的远距离通信。受电离层中存在瑞利衰落、多径效应、多普勒频移等复杂时变因素的影响，短波通信设备在测试和定装工作耗费较大。为了测试各种短波无线通信系统的性能，通常有两种方法，一种是实验测试，另一种是信道模拟。在实验测试中，为了测试短波通信设备的性能，往往需要在实际通信环境中进行大量的、远距离的场外实验和长时间的测试，实现起来非常困难；信道模拟方法则是通过对信道特性进行理论分析，建立信道模型，在实验室环境下进行与实际信道类似的模拟，它可以很容易地制造各种典型信道特性环境和电磁环境，能够模拟的地域度非常广阔，不受气候条件限制，可以随时进行多次重复实验，而且测试费用少，可以缩短通信设备的研制周期。在各种典型短波信道模型中，Watterson模型由于大多数情况下能够较好地反映短波信道的特性，且复杂度低，而被CCIR推荐并广泛使用。
在研究短波信道中有一个重要问题，即是多径的传播问题。多径传播主要带来两个问题：衰落和延时。多径延时是指多径中最大的传输延时与最小的传输延时之差。多径 时延 在短波线路上，最严重时时延可达到毫秒级。短波信道模拟器研究中，由于要求的延时尺寸比较大，而且延时的精度要尽可能的高，再加上实时性的原因，数据量非常大。为了后续的 DSP 的算法处理和前面A／D的数位和精度要求，可以选用大容量存储器作大尺度的延时处理，并选用DSP作插值算法做高精度的小尺寸的延时算法处理。本文重点对高精度小尺寸延时算法进行研究，提出一种基于内插技术的实现方法。
1 内插抽取器实现结构
整数倍内插就是指在两个原始抽样点之间插入I－1个零值。原始序列x(n)内插后的序列和频谱分别为：
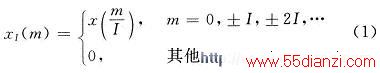
由式(2)可见，内插后信号频谱为原始序列谱经I倍压缩后得到的谱。在频谱图中不仅含有X(ejω)的基带分量，而且还含有其频率大于π／I的高频成分(称其为X(ejω)的高频镜像)。为了从XI(ejω)中恢复原始谱，则必须对内插后的信号进行低通滤波(滤波带宽为π／I)，经过内插大大提高了信号的时域分辨率。整数倍抽取是指把原始采样序列x(n)每隔D-1个数据取一个，以形成一个新序列xD(m)，即：
式中：D为抽取倍数，是正整数。xD(n)的离散傅里叶变换为：
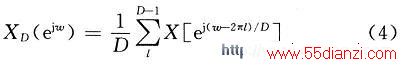
从式(4)可以看出，抽取序列的频谱XD(ejω)为抽取前原始序列频谱X(ejω)经频移和D倍展宽后的D个频谱的叠加和。如果x(n)序列的采样率为fs，则其无模糊带宽为fs／2。当以D倍抽取率对x(n)进行抽取后，得到的抽取序列xD(m)的取样率为fs／D，其无模糊带宽为fs／(2D)；当x(n)含有大于fs／(2D)的频率分量时，xD(m)就必然产生频谱混叠，导致从xD(m)中无法恢复x(n)中小于fs(2D)的频率分量信号。为了避免抽取带来的频谱混叠，需要用一数字滤波器(滤波器带宽为π／D)对X(ejω)进行滤波，使X(ejω)中只含有小于π／D的频率分量，再进行D倍抽取，则抽取后的频谱就不会发生混叠。可以说XD(ejω)能准确地表示X(ejω)中小于π／D的频率分量信号，所以这时对XD(ejω)进行处理等同于对X(ejω)的处理，但前者的数据流速率只有后者的1／D，大大降低了对后处理速度的要求。
前面介绍的抽取和内插的结构对运算速度的要求是相当高的，这主要表现在抽取滤波器模型中的低通滤波器位于抽取算子之前，也就是说低通滤波器是在降速之前实现的；而对于内插器模型，其低通滤波器位于内插算子之后，也就是说内插器低通滤波器是在提速之后进行的。总之，无论是抽取器还是内插器，其抗混叠数字滤波均在高取样率条件下进行，这大大提高了对运算速度的要求，对实时处理是极其不利的。下面将讨论有利于实时处理的抽取器、内插器的多相滤波结构。
设数字滤波器的冲击响应为h(n)，它的z变换定义为：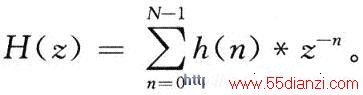
式中，N为滤波器长度。如果将冲激响应h(n)按下列的排列分成D个组，如N不为D的整数倍，则将h(n)后补零，使得滤波器长度N为D的整数倍，即N／D=Q，Q为整数，则：
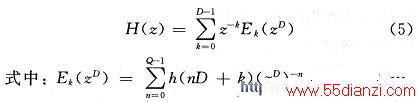
D-1。式(5)即为数字滤波器H(z)的多相滤波结构。针对本文的应用，此处给出一个I倍内插器多相滤波结构的实现框图，如图1所示。其中，Rk(z')=E(I-1-k)(z')。
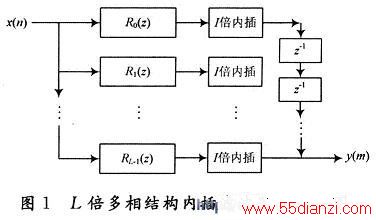
由图1可见，此时的数字滤波器Rk(z)位于内插器之前，即滤波是在数据流提速之前进行的，这就大大降低了对处理器的要求，提高了实时处理能力。此外，多相滤波器结构的另一个好处是每一分支滤波器的系数由原来的N个减少到N／I个，可以减小滤波运算的累积误差，有利于提高计算精度，降低对处理器字长的要求。图2是多相结构内插滤波器的开关结构形式。它可以更清楚地说明多相结构内插滤波器是如何工作的。对输入速率为Fs的数据流，经L个子滤波器后，每个子滤波器的数据流速度依然是Fs，但整个内插滤波器的数据流速度提高为I·Fs，此时用速率为I·Fs的开关对输出数据流进行选择，即完成了I倍内插数据的获取。同样可以得出D倍抽取器多相滤波结构。
2 时延 算法的 DSP 实现
短波信道模拟器系统中常采用软件无线电思想实现。软件无线电的宗旨就是尽可能地简化射频模拟前端，使A／D转换尽可能地靠近天线去完成模拟信号的数字化，而且数字化后的信号要尽可能多地用软件进行处理，实现各种功能和指标。软件部分主要用DSP芯片来进行处理信号。根据软件无线电的知识，可以使用内插来完成精确性时延部分的工作，但为了避免插值后数据量的大增，导致DSP处理的负荷量过重，之后就得考虑数据的抽取操作用以减少处理的数据量。在上部分中，可以得出内插和抽取过程都需要一滤波器进行滤波，避免内插带来的高频镜像和抽取带来的频谱混叠。可以采用内插和抽取组合的办法来解决内插所导致的数据量大增问题，并保证小尺寸时延的精度。但必须内插在前，抽取在后，以确保其中间序列的基带谱宽度不小于原始输入序列谱或输出序列谱的基带频谱宽度，否则将会引起信号失真。这里采取的是D倍内插再D倍抽取以实现级联来满足要求。但是由于他们级联的D倍内插滤波器和D倍抽取滤波器工作在相同的采样率Dfs下，所以他们可以以一个组合滤波器来代替。图3是基于内插和抽取技术的时延器结构。
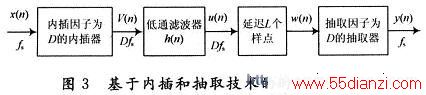
输入信号x(n)的抽样速率为fs，为实现延迟L／D个样点间隔，首先将x(n)的抽样速率增加到原来的D倍(即在x(n)的二个样点间插入D-1个零)，速率提高后的V(n)序列经低通滤波器滤波，低通滤波器的作用是滤除间隔为原抽样频率重复出现的成分。V(n)是x(n)内插后的序列，其抽样速率为Dfs，u(n)在高抽样率上延迟L个样点后得ω(n)，最后在ω(n)序列中，每D个样点保留一个即得到y(n)。y(n)是x(n)延迟了(L／D)T的序列，这里T=1／fs是原序列的抽样周期。在得出u(n)的过程中，经过的低通滤波器是 FIR 滤波器，V(n)序列经低通滤波器滤波时是利用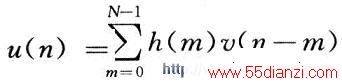
本文关键字：暂无联系方式DSP/FPGA技术，单片机-工控设备 - DSP/FPGA技术
