其中 δ(k)在k=0时取值为1,否则取值为0。
c.附加条件
条件(8)和条件(9)相当于N/2+1个独立的方程。为了确定N个滤波器系数,至少还需要N/2-1个独立的方程,因而需要附加其他条件。Daubechies施加的附加条件使得尺度函数能够精确地描述阶数不超过N/2的多项式,并且尺度函数与其对应的小波函数是相互正交的,相应的滤波器系数应满足的条件为:
![]() (11)
(11)
实际上,条件(10)是不独立的,因为它可以由其他已知的条件导出。上述约束条件唯一地确定了构造紧支撑正交小波所需的滤波器系数。特别地,当N=4时对应的滤波器系数如下:
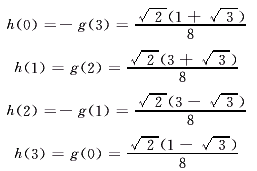
相应的小波函数称为D4小波。本文将D4小波用于输电线路故障暂态行波信息的压缩。
1.3 离散小波变换
任一非平稳信号s(t)在尺度j下的离散小波变换可以表示为该信号与尺度j下小波函数的内积,即:
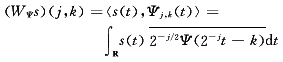 (12)
(12)
由于实际得到的信号往往以离散序列的形式出现,而且某些情况下(如紧支撑正交小波),小波函数不存在解析表达式,因而在实际应用中并不直接由式(12)对信号实施离散小波变换。对于正交小波,可以直接采用建立在多分辨分析基础之上的Mallat算法[17]实现快速离散小波变换,并可重构出原始信号序列。Mallat算法在小波分析中的地位相当于FFT算法在经典Fourier分析中的地位,以下对这一算法进行简要描述。
假定非平稳信号s(t)在零尺度下的离散逼近c0(n)为已知,并且可以用对该信号的采样序列s(n)来近似代替,即:
c0(n)=s(n) n=0,1,…,N-1 (13)
其中 N=2J;J∈N。
则序列c0(n)可以分解为一个小波系数序列d1(n)和一个逼近系数序列c1(n),对后者进行同样的分解可得一组新的小波系数和逼近系数。一般地,设序列cj-1(n)为信号在尺度j-1下的逼近系数,它经过分解可以得到尺度j下的小波系数dj(n)和逼近系数cj(n),前者含有信号中较高的频率成分(陡的边沿、拐点及突变点等),而后者则含有信号中较低的频率成分(大致轮廓),具体表示如下:
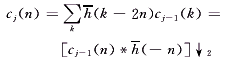 (15)
(15)
其中 “*”表示卷积(下同);“↓2”表示从滤波后的序列中抽取出第偶数个样点。
对于D4小波,由于其滤波器系数均为实数,因而各滤波器系数之间存在以下关系:
注意到每分解一步,所得小波系数和逼近系数的数据个数将各自减少一半,因此原信号最多可以被分解为log2N个尺度。从j=1,2,…,J(1≤J≤log2N)一直分解下去(每一尺度下的分解都以该尺度下的逼近系数为对象),则可实现信号的多尺度分解。
另一方面,原信号序列也可以通过尺度j(j=1,2,…,J)下的小波系数dj(n)和尺度J下的逼近系数cJ(n)得到重构,相应的重构算法为:
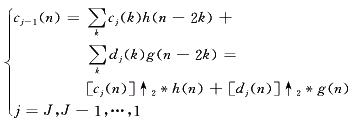 (17)
(17)
其中 “↑2”表示在序列中每相邻两个采样点之间插入一个数值为0的采样点。
以上分析表明,Mallat算法并不要求知道具体小波的表达形式,而只需给定两组滤波器系数即可。
2 基于小波分析的信号压缩方法
前面已经提到,信号序列经过Mallat算法的每一级分解后所得的小波系数和逼近系数个数将各自减少一半,因此最终保留下来的系数总数与原信号序列的数据个数相同。实际上,每一尺度下的小波系数并非均匀分布的,其中对应于信号奇异点的小波系数幅度比其他小波系数幅度大得多。由于输电线路故障产生的暂态行波信息主要蕴涵于信号奇异点中,因而可以舍弃幅度较小的小波系数(通过设置简单的门限来实现),这就实现了信号压缩。
为了重构原信号序列,还需要保留最终尺度下的逼近系数及各尺度下保留下来的小波系数所在位置,其中小波系数位置参数占有与小波系数本身同样多的存储单元。尽管重构时信息会有所损失,由于绝大多数被丢弃的小波系数与信号的奇异性无关,因此重构质量还是很高的。此外,重构后的信号序列中基本上不含有电气噪声,而且所保存的数据具有比原信号序列更加明确的意义,因此经过压缩还达到了整理数据的效果。
图1给出了离散信号的压缩及重构流程,其中每一尺度下信号压缩所采用的门限值不同,并且具有一定的自适应性。
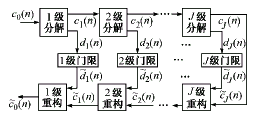
图1 离散信号的压缩与重构
Fig.1 Compression and reconstruction
of a discrete signal
某一尺度j下的门限值ηj可以表示为:
ηj=(1-u)×max{|dj(n)|,n=1,2,…,N/2j} (18)
其中 j=1,2,…,J;N为原信号序列长度(即信号在零尺度下的采样点数);J为压缩级数(即小波分解的最终尺度);u为调节参数,0≤u≤1,若u=0.9,则ηj为尺度j下小波系数最大幅值的10%。
信号经J级压缩处理后可以得到:
![]() (19)
(19)
设信号经过J级压缩后在某一尺度j下保留下来的小波系数个数为Nj,则最终需要保存的数据个数为:
其中 第1项表示经过压缩后各尺度下的小波系数及其位置参数的数据个数;第2项表示尺度J下逼近系数的数据个数。
信号的压缩比定义为:
信号重构后的瞬时误差定义为:
![]()
本文关键字:暂无联系方式电工文摘,电工技术 - 电工文摘