摘 要：提出了一种描述机动目标运动状态的自适应高斯模型，在这种模型中，机动目标的加速度被认为是具有非零均值、时间相关的随机过程，并假定其概率密度函数服从高斯分布。指出了机动目标运动模型的均值和方差与目标机动加速度最佳当前估计值之间的关系，在此基础上，提出了相应的自适应卡尔曼滤波算法。仿真结果表明，该算法对机动目标在不同机动方式下的位置、速度和加速度均有良好的跟踪效果，且所需计算量小。
关键词：机动目标跟踪；卡尔曼滤波；自适应高斯模型；算法；蒙特卡罗仿真
一、引言
30多年来，就机动目标的运动模型问题国内外进行了许多研究，取得了一些有益的结果：1970年，R. A. Singer［１］提出了机动目标的零均值、一阶时间相关机动加速度模型，目标的机动加速度表示为随机状态噪声驱动的结果，并由此建立起机动目标运动的统计模型；1979年，R. L. Moose［２］等人提出了具有随机开关均值的半马尔可夫机动目标统计模型，该模型在Singer模型的基础上进了一步；1981年，J. D. Kendrick［３］等人提出了一种基于采用辅助的电子光学系统进行目标姿态检测的交互作用滤波系统，对目标的运动姿态以及位置、速度、加速度等数据同时进行估计；1983年，R. F. Berg［４］提出了修正的Singer模型，该模型在Singer模型的基础上引进了加速度均值的时间导数项；我国学者周宏仁博士［５］于1983年提出了机动目标的“当前”统计模型，该模型在Singer模型的基础上引进了加速度的均值项，并采用修正的瑞利－马尔科夫过程描述目标机动加速度的统计特性；1984年，H. A. P. Blom［６］提出了交互式多模型（IMM）机动目标跟踪算法，其后，由Blom和Barshlom［７，８］等人合作完成了理论上较为完整的IMM算法。IMM算法用马尔可夫链过程描述模型间的转换，同时导出Kalman滤波输入输出均加权的交互式算法；1989年，张伯彦［１０］等提出了机动目标加速度的非零均值、时间相关的截断正态概率模型，在这种模型中，机动目标的加速度被认为是具有非零均值、时间相关的随机过程，并将它的概率密度函数假定为截断正态型。
本文提出一种描述机动目标运动状态的新模型机动目标自适应高斯模型。假定机动目标的加速度为一高斯－马尔科夫过程，高斯分布的均值为目标机动加速度的最佳当前估计值，由于高斯分布的方差是描述随机变量的散布性指标，所以在本模型中取其值与目标机动加速度最佳当前估计值的导数相关。其物理意义是：在对目标机动特征无任何先验知识的条件下，认为目标的机动加速度服从高斯分布，其真实加速度在加速度估计值附近取值，高斯分布的散布性指标反映在目标加速度估计值的离散性之中。
二、自适应高斯模型
1.非零均值一阶时间相关模型
在机动目标运动中，其机动加速度不可能总是一平稳的随机过程，设目标机动加速度是一非零均值的时间相关随机过程，即
设a(t)的时间相关函数为指数衰减形式［１］：
式中
为目标机动加速度的方差；a为目标机动时间常数的倒数，即机动频率。、a均为在区间（t，t τ）内决定目标机动特性的待定参数。
在目标跟踪中，卡尔曼(Kalman)滤波器要求用高斯(Gauss)白噪声作为驱动噪声，(1)式表示的模型不能直接应用于Kalman滤波器，故需对(2)式所表示的零均值有色加速度噪声的相关函数作Wiener-Klmogorov白化处理，将有色噪声a(t)表示为白噪声ω(t)驱动的结果。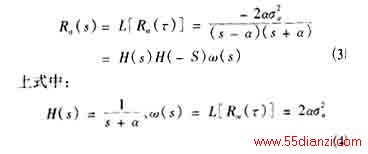
(4)式中Ｒω（τ）为白噪声ω(t)的相关函数，其值为
。
由以上推导得一阶平稳相关Markov过程、即机动加速度的零均值一阶时间相关模型a(t):
其中输入白噪声ω(t)的方差为
由(1)和(5)二式
可得机动加速度的非零均值一阶时间相关模型：
2自适应高斯模型
在对目标机动加速度的统计特征无任何先验知识的前提下，可假定(7)式所描述的机动加速度非零均值一阶时间相关模型的概率密度服从均值为、方差为
，同时有
。
根据高斯分布的性质，加速度(t)的概率密度函数为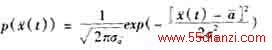
根据估值理论，目标机动加速度的均值取在观察量z(t)条件下机动加速度的条件期望值，即状态变量(t)的最佳估计值；高斯分布的方差是描述随机变量的散布性指标，令：
导数，b为方差自适应系数，取常数值。
根据高斯分布的性质，当分布函数的均值和方差两个特征数字确定后，便唯一地确定了一个高斯分布，故由(8)式确定了目标机动加速度自适应高斯模型中机动加速度的概率密度分布。由(7)
