式、
(8)式和
(9)式组成机动目标加速度的自适应高斯模型。
三、跟踪算法
为使问题阐述简单起见,仅考虑直角坐标系下一维坐标的跟踪算法,其他两维类推。
由
(7)式得,跟踪系统的状态方程为


分别表示目标的位移、速度、加速度和加速度均值

。
设采样周期为
T,对
(10)式所表示的系统连续状态方程进行离散化,得
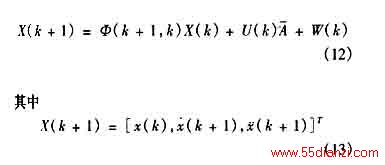
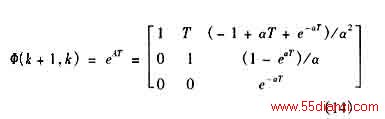

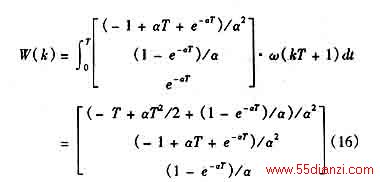
设跟踪系统的量测方程为
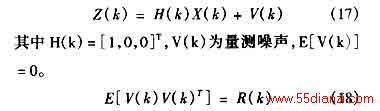
由
(12)式和
(17)式所表示的系统的
kalman滤波方程为
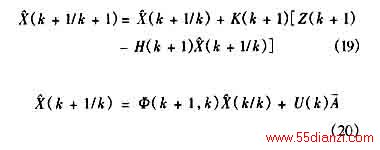

其中
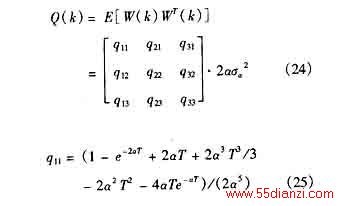



则由
(19)~
(33)式构成了由
(12)和
(17)式所表示的系统的基于自适应高斯模型的跟踪算法。
四、蒙特卡罗仿真
为评价本文提出的机动目标自适应高斯模型的性能、且便于和其它几种经典的机动目标模型进行比较,作者就水下环境中的几种典型目标机动形式进行了蒙特卡罗
(Monte Carlo)比较仿真研究。仿真中的参数及初值选取如下:
(1) 目标常速直线机动时
 (3)
(3) 目标蛇形机动时
x(0)=500
m,
y(0)=0、
h(0)=0,α
max=10
m/s2,α=0.1,T=1。目标沿
x轴方向蛇形机动,机动幅度为
500 m,机动角频率为
2π
/200。
观测噪声方差均取值为
r(t)=(0.03x(t) 5)2
m2。在仿真研究中,作者分别将文献[
1]、[
5]、[
10]中提出的
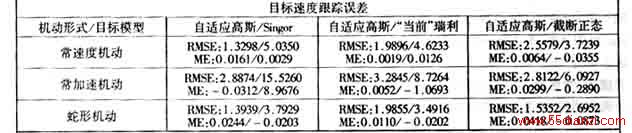
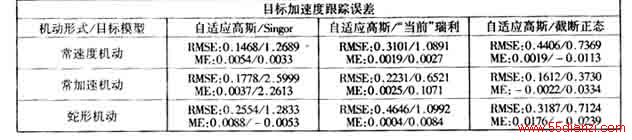
Singer模型、“当前”统计模型、截断正态概率模型在目标分别作常速度、常加速度、蛇形机动3种机动形式下,与本文提出的机动目标自适应高斯模型进行了9组
Monte Carlo比较仿真试验,每组仿真试验各做
60次,仿真结果见表
1。限于文章篇幅,作者仅在图
1和图
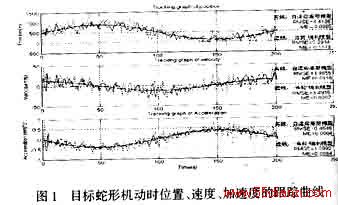
2中画出了自适应高斯模型和“当前”统计模型在目标分别作蛇形机动和常加速度机动时的位置、速度和加速度跟踪曲线。图中“
RMSE”代表均方根误差,“
ME”代表均值误差。为便于观察,作者对图中的跟踪误差进行了等比例放大处理。

 3
3
从图1和图2可看出,在水下目标运动环境下,无论目标作蛇形机动,还是作常加速机动,本文所提出的机动目标自适应高斯模型在对目标位置、速度和加速度的跟踪方面,均比文献[5]所提出的机动目标“当前”统计模型有较小的均方根误差和均值误差;从表1可看出,本文所提出的机动目标自适应高斯模型对机动目标的不同机动形式均有很好的自适应能力,且跟踪误差优于所比较的几种机动目标模型。
五、结论
本文在深入研究机动目标运动特征和目标模型的基础上提出了机动目标自适应高斯模型,理论分析和Monte Carlo仿真结果表明:在机动目标自适应高斯模型中,加速度分布均值和方差的选取充分体现了目标的机动特征和高斯分布中均值和方差的物理意义;在对目标机动特征无任何先验知识的条件下,本文所提出的机动目标自适应高斯模型能很好地适应目标的不同机动形式;与Singer模型、“当前”统计模型和截断正态概率模型相比,在水下机动环境下,自适应高斯模型对机动目标的位置、速度和加速度均具有良好的跟踪精度,且运算量小,适合于对复杂机动情况下的目标进行实时精确跟踪。
参考文献
[1]R A Singer. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets[J].IEEE Transactions on Aerospace and Electronic Systems, 1970, 6(4): 473~483.
[2]RLMoose, H F Vanlandandingham,D H Mecabe. Modeling andEstimation for Tracking Maneuvering Targets
上一页 [1] [2] [3] 下一页
本文关键字:模型 高斯 电工入门,电工技术 - 电工入门

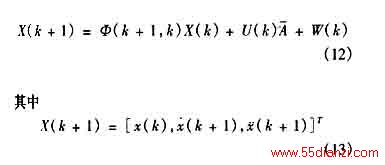
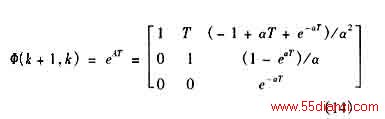

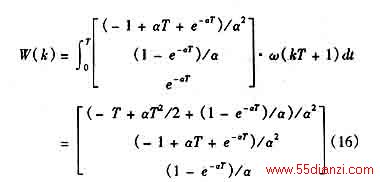
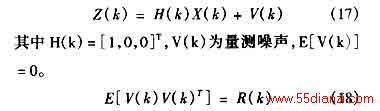
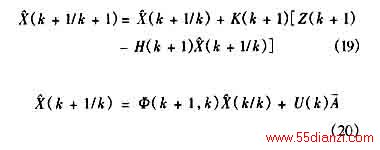

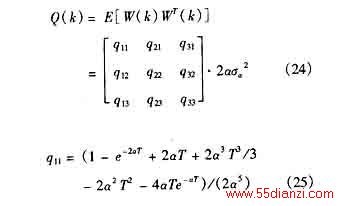








 3
3