1 引言
电力电子电路拓扑的研究在电力电子学中占据重要地位。长期以来,新电路拓扑的创立过程主要依赖于灵感和经验,没有严密并可以遵循的逻辑和模式[1-2]。以图论为基础的拓扑推演方法可以从拓扑学的角度深刻揭示各种不同拓扑之间的内在联系,试图采用拓扑推演的方法生成新拓扑。这是近年来关于如何进行电路拓扑研究的一种新思路[3]。
在拓扑推演的过程中首先遇到的问题是要确定有效的研究范围。而其中所依据的原则或判定条件十分关键,如果判定条件不合适可能会将有用的电路拓扑遗失或存在大量的无用拓扑影响判断效率。在优化研究范围时,可以采用两方面的条件加以约束:
(1)结构条件。将混合开关拓扑抽象为图。通过数学方法将所有的同构拓扑找出来,生成一组最大非同构混合开关拓扑空间基底,将结构重复的拓扑剔除。这也是本文的主要工作。
(2)电路定理条件。现代电路拓扑研究起源于基本电路定理的建立,包括KCL、KVL、互易定理和特勒根定理等基本电路定理,它们都是以电路拓扑的研究为基础的。通过电路定理条件判定将不符合电路原理的拓扑剔除。
通过以上两个条件的判定,可以将拓扑推演的研究范围确定下来。剩下的工作就是依据电力电子电路的特点导出具体拓扑。关于如何在电路定理条件判据下,确立研究范围已经在一些文献中有所体现[3-4]。而关于结构条件判定的研究工作尚不多见。
同构混合开关拓扑的辨识可以归结为图的同构问题。图的同构问题是图论中需要研究的一个重要问题,同构图的判定在机械设计、模式识别、电路设计等方面有很广泛的应用[5-8]。本文依据现有的简单图的同构判定方法提出了同构混合开关拓扑的辨识算法。并作了算法验证,验证实例证明辨识方法是正确和有效的。
2 混合开关拓扑的定义和数学描述
2.1 混合开关拓扑的基本概念
开关拓扑是对含有电容、电感和开关元件的电力电子电路的抽象。其中电容和电感元件可以抽象为理想的线性电容和电感元件。在一定条件下,较大的电容和电感元件可以进一步等效为电压源和电流源,开关元件可以抽象为理想开关。考虑到效率的因素,在电力电子电路中电阻元件通常作为负载或是在保护、采样电路中出现。因此在开关拓扑中一般不含电阻元件。由电容、电感、开关元件、电压源和电流源组成的开关拓扑被称之为混合开关拓扑。
图1是一个典型的零电压转换(Zero-Voltage-Transition—ZVT)PWM软开关升压斩波电路的理想化拓扑,电路中的节点即为图的节点,电路中的元件即为图中的支路。
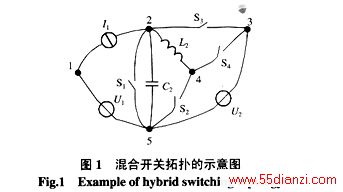
混合开关拓扑可以分解为单属性支路网络,它们分别是电容网络、电感网络、电压源网络、电流源网络和开关网络等。比如,图1所示的混合开关拓扑可以分解为图2-(a)至2-(e)所示的5个网络。

2.2 混合开关拓扑的数学描述
2.2.1 概述
只有建立混合开关拓扑的准确数学描述,才能方便地使用各种数学方法和工具处理拓扑的相关问题。混合开关拓扑可以采用图、矩阵和编号的方式描述。图的优点是形象、直观,缺点是不便于数学处理。矩阵和编号的描述方式则更利于数学处理。
2.2.2 基于单属性支路网络的矩阵和编号表示方法
(1)矩阵表示方法
对于一个由单一属性的支路构成的节点数为n的网络,设其任意两节点间最多仅存在1条支路,其邻接矩阵A定义为一个 n×n的方阵,其元素为
![]()
混合开关拓扑有电容、电感、电压源、电流源和开关等5种不同的单属性网络,因此可以分别写出它们对应的邻接矩阵:AC、AL、AU、AI、AS。举例来说,图2中5个不同的5节点网络的邻接矩阵分别为
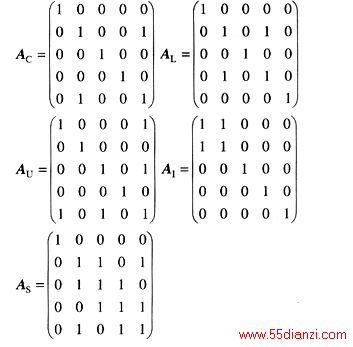
而一个拓扑T总能表示为5个邻接矩阵的组合:T=(AC,AL,AU,AI,AS)
(2)编号表示方法

式中 aij是n节点网络的邻接矩阵元素,其定义如式(1)。
这样,D=dmdm-1dm-2...d2d1d0就构成了一个m位的二进制数,D值的范围是0~2m-1,且D值同该网络的邻接矩阵一一对应。根据网络的邻接矩阵,可以根据式(2)计算其D值;而每给出一个D,就可以根据式(2)写出其对应的邻接矩阵,并能画出该网络的图。这样就用编号的方法完成了对网络的描述。
对于5种不同单属性的网络,可以用式(2)所定义的方法建立各自网络的编号DC、DL、DU、DI、DS。图2中各网络的编号为

2.2.3 基于混合支路的矩阵和编号表示方法
基于混合支路的矩阵和编号表示方法,是建立在对支路的抽象和编号的基础上的。混合支路指混合开关拓扑中由单开关、电压源、电流源、电容、电感或是其中的某些元件并联组成的支路。图3所示为一种混合支路。在基于混合支路概念下的混合开关拓扑可以抽象为不含复边和自环的简单图。每条边含有不同的权值,蕴含着边的信息。
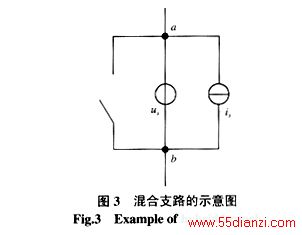
图4列出了所有支路可能的组合,一共是32种。按如下规则进行编码:
(1)采用二进制编码,支路包含有5种元件,所以为五位二进制编码。当支路包含有该元件时,该位为1,否则为0。
本文关键字:开关 电源,电工技术 - 电源