1 引言
配电网络重构通过改变网络拓扑结构来获得运行效益最优的运行方式,其研究内容可分为两大类:
第一类是针对恒定负荷的静态重构,主要方法有启发式方法,如支路交换法[1]、最优流模式法等;传统数学优化方法,如线性整数规划法、分支定界法等;智能计算方法,如模拟退火法、神经网络法、遗传算法等。第二类是时变重构(也称动态重构),是在负荷不断变化的情况下求解一段时间内的重构方案。主要方法有启发式方法[2, 3],启发式方法与智能计算方法相结合的混合算法[4],等等。
实际配电系统负荷变化频繁,静态重构只给出开关设备一个时刻的动作方案,各时刻间的优化方案缺乏联系,所以缺乏实用性。静态重构属于大规模、多目标、非线性、混合整型、组合优化问题,属于NP难问题,显然,针对给定时间区间的时变重构问题时间复杂性和空间复杂性更高。目前见诸文献的方法根据启发式规则只提供了局优解。
本文以中压配电网络为研究对象,提出了以运行费用最小为目标的时变重构全局优化算法。
2 数学模型
本文算法的目标函数可表示为
![]()
式中 F、NB和N分别为给定时间区间内的运行费用(包括开关操作费用和电能损耗费用)、可操作的开关总数和所划分的时间段总数;xk,i为开关k在第i时段的状态,取值为0或1,分别为开关处于断开位置和闭合位置;xk,0为开关k的初始状态;PLi为第i时段系统的有功功率损耗,kW;ti为第i时段的长度, h;CBk、CLi分别为开关k操作一次的费用,元和第i时段的网损电价,元/kWh。
重构后的网络应满足潮流方程约束、各种安全约束和放射状运行约束。此外,时变重构问题还必须满足开关操作次数约束,即在所研究的时段内满足式(2)所描述的系统中所有可操作开关总的操作次数限制和式(3)所描述的单台开关的操作次数限制。
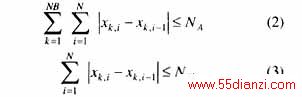
式中 NA、NSk分别为给定时间区间内最大允许的总的开关操作次数和开关k最大允许的操作次数。
3 时变重构全局优化算法
3.1 算法步骤
为了在给定时间区间内实现中压配电网的运行费用最小,本文算法进行如下操作:
(1)计算与识别网络的初始信息,包括节点电压、支路功率、有功损耗、开关状态,等等;
(2)将给定的时间区间划分为多个时间段。在每个时间段内,根据负荷预测的结果将负荷近似为恒功率负荷。以网损最小为目标,使用核心模式遗传最短路算法求解静态重构子问题,得出多个候选的可行放射状网络结构。
(3)根据上步得出的各个时段的可行放射状网络结构,应用动态规划,求解运行费用最小的全局最优时变重构策略。
可见,本文算法包含核心模式遗传最短路算法和动态规划两个核心,下面分别予以说明。
3.2 CSGSA求解静态重构子问题
用无向元件网络图G来表示所研究的中压配电网,BS
和LS分别表示支路集合与负荷节点集合。大部分见诸文献的重构方法是针对BS进行操作的,试图找到BS的一个子集BS¢'⊂BS,使得BS¢中的所有支路组成一个满足各种约束条件的放射状运行网络,这类方法被称为组合支路法。CSGSA基于组合负荷的思想,其研究对象为LS而非BS,通过为LS中的每个负荷分别寻找供电路径来逐步获得放射状网络结构。负荷寻路的先后次序决定结果网络,CSGSA就是在使用遗传算法搜寻最优的负荷寻路次序的过程中并行得出多个可行的放射状网络结构。CSGSA以网损最小为目标,算法流程如图1所示。
图中第(1)步为将LS中的负荷表示成负荷串的形式,其排列次序即为负荷寻路的先后次序;
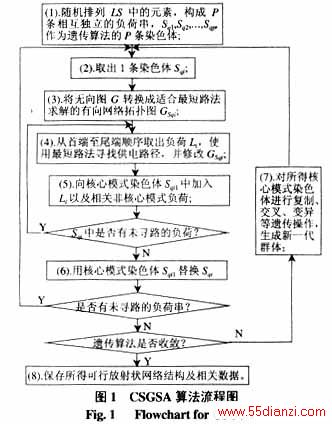
第(3)步为形成有向网络拓扑图![]()
第(4)步为使用最短路法在GSqi中搜寻当前负荷的最佳供电路径。所用弧权值公式定义为

式(4)的作用是使寻路过程中网损增量相对较小,剩余容量相对较大的弧优先被选中,从而平衡结果网络各个支路的负荷,避免由于先寻路负荷的供电路径过于集中而导致的后寻路负荷无法找到合法供电路径的现象;
第(5)步至第(7)步的理论基础是遗传算法的模式定理。研究发现,根据Sqi中负荷排列的先后次序可将LS分解为2个互补的子集LS¢Sqi与LS²Sqi,其中,LS¢Sqi中的负荷被称为核心模式负荷,它们对放射状网络结构的生成起着关键性的影响。LS²Sqi中的负荷被称为非核心模式负荷,它们通过改变GSqi中的支路权值来影响后续负荷的寻路结果,因此对网络结构的生成也有影响,但该影响是次要的。例如,对Sqi中的负荷Li寻路,将得到供电路径P。假设P上存在还未使用最短路法寻路的负荷Lα1, ···, Lαα,根据配电网络的放射状约束易知,其供电路径已由Li确定,因此有:![]()
本文关键字:暂无联系方式电工技术,电工技术 - 电工技术