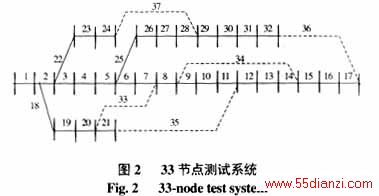
大量计算表明,针对不同的初始结构和时间区间,算法总能找到从初始结构过渡到最优结构的费用最小重构方案。当网络负载率不高时,网络调整到最优结构后,如果负荷的模式如类型、峰荷大小、负荷曲线等没有太大的变化,则不需再进行任何重构操作,网络结构将保持最优,这为季节性重构提供了参考。例如,在上述网络和负荷模式下,最优网络结构选择线路7,9,14,28,36作为联络线。
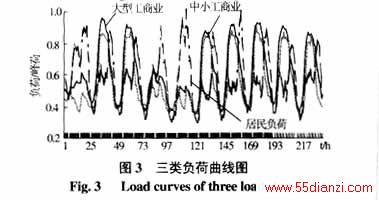
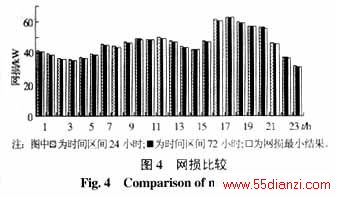
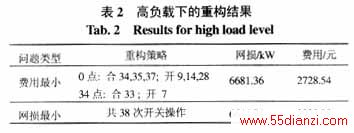
设初始网络结构选择33~37作为联络线,使用本文算法进行时变重构优化计算,第1种情况为将24h作为给定时间区间进行计算,优化结果作为下次计算的初始网络结构,连续计算3天;第2种情况为将3天作为给定时间区间进行优化计算。两种情况的计算结果见表1。可见,给定的时间区间不同,可能导致优化结果的不同。如果初始网络结构与最优结构相差较大,由式(1)可知,时间区间长,则开关操作费用在总费用中的比例小,优化结果趋于最优网络结构;时间区间短,则算法将逐步向最优结构过渡,以保证当前时间区间内的费用最小。表1即说明了2种情况到达最优结构的路径不同,第1种情况的前24h属于过渡阶段,后48h重构为最优结构。第2种情况只在0点重构一次便使得72h内运行费用最小。图4为前24h的网损比较。图中还给出了不限制开关操作次数的网损最小结果,网损为4610.71kW,72h里需要进行26次开关操作,费用为2026.28元。可见,本文算法所得结果的网损与网损最小值非常接近,但费用却显著减少。以上虽然对不同时间区间的优化结果进行了比较,但实际应用中,若网络负载率不高且当前负荷模式维持足够长时间时,将选择一步重构到当前负荷模式下的最优网络结构,而不必经过若干过渡。如果网络的负载率很高或负荷变化剧烈,那么网络结构应进行相应调整以保证满足电压或容量等约束条件。表2给出了当每个节点的负荷都增长19%时的重构策略,同时给出相同情况下的网损最小结果。
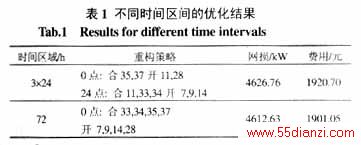
如果开关可操作次数很少,无法重构到最优的网络结构,则算法将得出满足开关操作次数约束的运行费用次优解。如表2所示的72h优化结果需要8次开关操作,如果限定每台开关只能操作2次,总的开关操作不超过4次,那么算法所得网络结构的联络线是11,28,33,34,36,从初始状态只需4次开关操作即可实现,网损为4698.25kW,费用为1907.30元。此外,若使开关操作费用为零,则算法转化为电能损失最小重构问题;若只考虑单一时段,则算法转化为静态重构问题;若只考虑单一时间点,同时开关操作费用为零,则算法转化为传统的静态网损最小重构问题。实际应用中可能遇到最优解不唯一或者有其它一些约束需要考虑的情况,这时,算法将动态规划寻优所得的所有可行重构策略由优至劣排序,然后全部输出,由用户来选择最终的方案。可见本文算法非常实用,应用范围非常广泛。
6 结语
实际配电系统负荷变化频繁,重构方案也应相应变化,本文给出了时变重构的全局优化算法,可在所研究的时间区间内实现运行费用最小化。算法主要由CSGSA和动态规划组成,并对开关操作次数约束进行了处理,使之不影响动态规划计算结果的全局最优性。大量计算表明:本文算法计算速度快,解的质量高,可用于配电网络的实时调度,可在降低运行费用的同时提高供电质量与供电可靠性,也可将之用于规划和离线分析等方面。
本文关键字:暂无联系方式电工技术,电工技术 - 电工技术