1 引言
现代电力系统中存在的低频振荡现象是增幅性低频振荡小干扰下系统失稳的主要原因之一。弱阻尼低频振荡模式是增幅性低频振荡发生的内在因素。所以,长期以来人们一直都把小干扰稳定分析的重点放在对低频振荡模式的研究上, 这个时期,低频振荡模式是与大干扰强非线性无关的。
向量场正则形理论作为分析非线性系统的一个新的有效工具,已被用来研究大干扰下stress系统的动态特性[1~4]。文[1]论证了2阶解在大干扰模式间的非线性相关作用的有效性,文[2] 在2阶解的基础上研究了模式间非线性相关作用对控制器性能的影响,文[3]利用模式间的非线性相关作用提出了确定经典电力系统模型临界切除时间的新方法, 文[4]推出了在谐振与准谐振条件下的2阶解析解,找到了大干扰下易失稳的参数域。向量场正则形理论突破了传统稳定分析的局限,把模式和大干扰下系统的动态特性联在了一起,而在电力系统中应用向量场正则形理论的关键是求解出非线性正则变换系数。
本文提出了数值求解向量场非线性正则变换系数的算法(ND算法),该算法简单、方便、实用、有效,适用于任何复杂的电力系统,给出了实用的鉴别主导低频振荡模式的方法。在此基础上,通过研究低频振荡模式与其它模式以及状态变量间的非线性相关作用,把低频振荡模式与系统大干扰稳定联系在一起,探索了低频振荡模式在大干扰稳定中充当的角色和作用,从另一个侧面揭示了以往大干扰稳定分析中所无法涉及的一些新现象,得到了一些新的观点和新的见解。
2 向量场的正则变换
移平衡点到原点,对n机系统,消去非发电机节点的N维状态方程为
![]()
式中 x为状态向量,Y
为电压和电流组成的中间变量。
若U为系统的右特征向量阵,取线性变换x=UY, 式(1)变为约当形系统![]()
式中 Y为约当形变量;J为由系统特征根组成的对角矩阵;Y2(Y)为系统的二阶项;Yh为高阶项。
向量场正则形理论指出,通过正则变换,约当形系统中的高阶项可以消掉,系统变为正则形[5]即线性系统如下:
![]()
式中 zj为正则形变量;lj为系统第j个特征根。

式(4)是非线性正则变换系数或称为非线性相关系数,它代表模式间非线性相关作用的大小。![]() 为矩阵C j的第K行第l列,
为矩阵C j的第K行第l列,
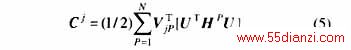
式中 V为规格化的左特征向量;VT=U-1;H P为原系统海森矩阵H的第P个子阵。
式(3)的解析解很容易写出,在式(3)解析解的基础上,再利用上述正则变换矩阵的反变换阵Z=Y-h2(Y),可得式(2)的2阶解析解[5]为

从上式可看出,模式仍是2阶解的主要成分,而非线性正则变换系数则是构成2阶解的一个基本参数,它包含着一系列重要的非线性信息,是展现系统非线性特性的源泉 [1,2,4]。要求得2阶解,其最重要、最关键的一步是求出非线性正则变换系数。
3 求解非线性正则变换系数的ND算法
由于电力系统的状态方程是由状态变量和中间变量y共同组成的,只有从状态方程、非线性网络方程和机端电压方程中消掉y,才能得到仅含状态变量的封闭的状态方程,进而解析求得系统的海森矩阵,再求得非线性正则变换系数。但由于非线性网络方程的存在,要从机端电压方程和网络方程中消掉中间变量y,得到封闭的不含y
的状态方程,是根本办不到的。按以往线性化方法得到的雅克比矩阵,也只是系统一阶偏导数在平衡点处的值,是无法继续求海森矩阵的。即使是走别的解析求导的渠道,也将是一件困难和繁杂的事情。所以,求取系统状态方程的高阶偏导数就成了研究大干扰下低频振荡模式作用的第一道难题。
本文避开了解析求导,在文[7]、[9]的基础上,提出了数值求解状态方程海森矩阵的算法(ND算法),不但成功地解决了第一道难题,同时因为ND算法具有简单方便,适应性强的特点,所以也为其它复杂系统求取高阶偏导数提供了一个有效的工具。

这里,特别要提及的是,f对状态变量的一阶偏导数是用解析方法求得的,以往小干扰稳定分析中任何一种解析求f雅可比矩阵A的算法都可用,数值微商处理的仅仅是2阶偏导,这是本文所提用数值微商求海森矩阵的精髓所在。
数值微商中另一个重要问题就是增量Dx的选取和误差分析。在式(8)中,x*是系统的原平衡点,一般情况下它不会是零,所以可以给定数值微商中第j个状态变量在平衡点处的增量Dxj为

则数值微商的截断误差应是O(10-8Dxj)=O(10-10)阶; 若取Dxj=10-5,则数值微商的截断误差应是O(10-10)阶, 而舍入误差是O(u/Dxj)=O(10-9)阶。这完全可以满足实际需要。
阶, 而舍入误差是O(u/ 求得系统的海森矩阵,再求非线性正则变换系数就只是简单的矩阵乘法运算的问题了。
本文关键字:暂无联系方式电工技术,电工技术 - 电工技术