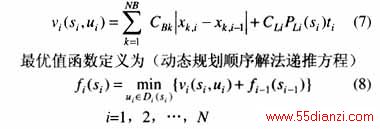最小化运行费用的时变重构全局优化算法

与L_S²Sqi中的负荷混杂形成染色体S_qi，先寻路负荷对后寻路负荷供电路径的搜索有着程序很难控制的复杂影响，因此该编码方式得出的染色体各基因的关系是强耦合的，具有高阶、长定义长度的特点，不适合遗传操作。
    第（5）步实现为S_qi寻路的同时，将L_S分解为L_S'Sqi和L_{S² Sqi}，从而突出核心模式负荷的作用，屏蔽非核心模式负荷的影响。具体操作如下：建立空的核心模式染色体，为S_qi中的负荷依次寻路的同时，剔除相关的非核心模式负荷，同时向中以从首端至尾端的顺序添加核心模式负荷，以从尾端至首端的顺序添加相关的非核心模式负荷，最后用所得到的核心模式染色体替换S_qi来参加遗传运算。所得S'_qi的模式如下所示：

式中  *为无需使用最短路法寻路的非核心模式负荷。
    的首段L_g1,…,L_gg∈L_S'Sqi由核心模式负荷组成，尾段由非核心模式负荷组成，负荷排列的先后顺序由其在S_qi中的相对位置决定。可见，该类染色体都具备低阶、短定义长度的特点，所以，通过选择、交叉和变异等遗传运算，一些较差的核心模式逐步被淘汰，一些较好的核心模式逐步被遗传和进化，最终可得到问题的最优解。这种方法不但大大改善了算法的收敛性，提高了搜寻最优解的能力，同时省去了为非核心模式负荷使用最短路法寻优的过程。通常，核心模式负荷数g远小于非核心模式负荷数β，因此，计算速度得到大幅度提高。
    通过计算得出的候选放射状网络结构成为动态规划求解全局最优时变重构策略的前提与基础。
3.3  以动态规划求解全局最优时变重构策略
3.3.1 动态规划数学模型
    动态规划是运筹学的一个分支，是求解多阶段决策过程最优化的数学方法。本文把给定的时间区间划分为若干阶段，将时变重构问题转化为多阶段决策过程，然后使用动态规划求解，其步骤为：
   （1）以时间划分阶段。将所研究的时间区间划分为N个时段，各时段长度可以相等，也可不等；
   （2）选择可行放射状网络结构作为动态规划中的状态(由网络中可操作开关的开合位置来表示)。第i时段的可达状态集合记为S_i。
   （3）时段间状态转移决策。U_i为第i时段状态处于s_i的决策变量，D_i为第i时段的允许决策集合， u_i(s_i)∈D_i(s_i)，T_i为状态转移函数。时变重构问题的初始状态已知，故根据s_i、u_i来确定s_i-1，有

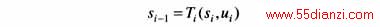
   （4）指标函数和最优值函数。
    选择开关操作费用和电能损耗费用之和为指标函数，其表达式为

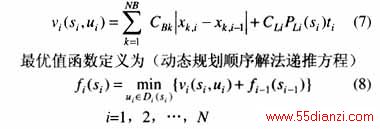边界条件为f₀(s₀)=0，即设定s₀为网络的初始状态，作为第0阶段，其费用为0。第1时段至第N时段为所研究的时间区间。
    从第0阶段开始递推求解，记录每个s_i的最优值函数及相应的s_i-1，最后从第N时段选出最优的s_N并回推得出全局最优的重构策略。
3.3.2 开关操作次数约束的处理
    为了限制开关操作次数，防止由于开关操作次数约束导致的无解或采纳局优解，应使某些相邻时段可以存在相同的网络结构，因为如果动态规划在相邻的时段选择了相同的网络结构，则表示时段间无需任何开关操作。动态规划各个阶段的状态由CSGSA计算获得，都是网损相对较小的网络结构，所以本文采取了状态锁定措施，目的是提供网损相对较大但所需开关操作次数较少的网络结构，也就是保证相邻的若干时间段中存在相同的可行放射状网络结构。状态锁定措施的具体步骤是：将当前时段的状态加入相邻的下一时段中，判断该状态是否已经存在，并计算状态是否可行，若该状态已经存在或是状态可行，则继续向后面相邻的时段添加该状态，若状态为不可行或是已经到达末时段，则终止当前状态的添加过程。状态锁定丰富了各个时段的状态数量，为限制开关操作次数提供了可能。
    在动态规划寻优过程中，如果某阶段状态给定，则此前各阶段状态决定了到目前为止已经操作的开关次数，若此时考虑开关操作次数约束，则意味着此前各阶段状态将影响该阶段以后状态的选择，这将导致状态变量不满足构造动态规划模型所必需的无后效性(马尔科夫性)条件。虽然采取适当增多状态变量的方法(如增加已操作开关数作为状态变量)，总能把过程变为无后效的，但这会大大增加算法的复杂性。考虑到本文算法的目标是最小化运行费用，其中包括了开关操作的费用，这就等价于隐性地限制了开关操作次数。加之状态锁定措施为限制开关操作次数提供了可能，因此，动态规划递推寻优过程中不考虑开关操作次数是否越限。当寻优过程结束后，选择运行费用最小的重构策略，这时再判断是否满足开关操作次数约束，若满足约束，则完成计算，得出全局最优时变重构策略。
    动态规划计算得出了多个可行重构策略，经过递推寻优过程之后，这些可行策略的运行费用是非常接近的，所以当费用最小解违反开关约束时，可以直接从所得的众多策略中选出满足开关约束的费用最小策略作为最终结果。开关操作次数越限往往只对应于给定的开关可操作次数非常少的极端情况。大量计算表明，本文算法所得费用最小解所需开关操作次数很少，一般情况下能够满足开关操作次数的约束条件。因为一方面，CSGSA通过全局寻优和局部寻优，能够快速得到每个时段的最优网络结构和大量的次优网络结构，状态锁定措施进一步丰富了各个时段可行网络结构的数量，使得每个时段都包含了足够的可行网络结构以供选择；另一方面，动态规划本身具备了全局搜索能力。所以，本文算法能够得到最优的和大量次优的时变重构策略，保证了算法的全局最优性。

上一页  [1] [2] [3]  下一页

本文关键字：暂无联系方式电工技术，电工技术 - 电工技术