7.1.2 虹膜内边缘的确定
如上所述,阈值分割可以初步地将瞳孔分割出来,但是考虑到算法的抗干扰能力,应对不同光照情况下阈值分割图像的差异情况予以充分考虑,对于光照均匀程度所带来的噪声与干扰也应能够很好处理。本文拟对阈值分割后的图像进行精确取点,然后采用hough 变换来确定圆的圆心和半径。
(1) 圆的Hough 变换
Hough 变换是对图像进行某种形式的坐标变换,它将原始图像中给定的形状的曲线或直线变换成变换空间的一个点,即原始图像中曲线或直线上所有点都集中到变换空间的某个点上形成峰点,这样,把原始图像中给定形状的曲线或直线的检测问题,变成寻找变换空间的峰点问题,也即把检测整体特性(给定曲线的点集)变成检测局部特性的问题。
由上述原理,可得圆的Hough 变换的方法:在x-y 平面上,中心在(
),半径是
的圆周C上一点(x,y)满足:

(7-1)
如果将圆心(a,b)看作为变量,则在a-b 平面上可以画出中心在(x,y),半径
的圆
。在圆C 上的每一点(
),在a-b 平面上有中心在(
,
),半径为rc 的圆
与之对应,且这些圆组成了相交于一点(
)圆群,进一步把圆的半径r 作为变量,在a-b 平面得到由不同半径的圆CHi 构成的圆环。在a-b-r 空间中建立三维数组,数组中元素 ai,bi,ri P 的值代表a-b 平面上通
过点(ai,bi),半径为ri 圆的个数。如果图像中存在满足方程(7-1)的圆,则
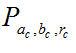
的值最大。即
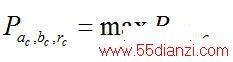
(7-2)
因此,数组中最大值元素所对应的参量(
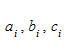
)就是图像中圆的中心和半径。
(2) Hough 变换的改进PHT 变换
上述变换方法虽然由使用广泛,但是因为它要在三维空间内搜索,计算复杂性较大,为此采用点Hough 变换,原理如图6所示,设K,L,M为圆周上三点,由圆的几何性质可知,KL 的中垂线L(KL) 与LM 的中垂线L(LM)必然相交于圆C 的中心O。设K、L、M 三点的坐标分别为
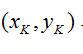
、
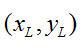
、
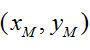
,则L(KL) 和L(LM) 的方程分别为:
L(KL):
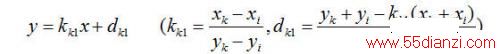
(7-3)
L(LM):
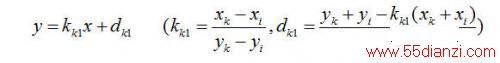
(7-4)
利用(7-3)和(7-4)式,计算出圆C 的圆心(
)和半径
:
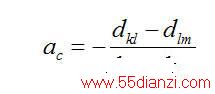
(7-5)
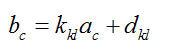
(7-6)
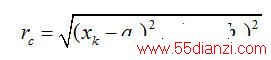
(7-7)
可见, 半径ri,中心(
本文关键字:加密 DSP/FPGA技术,单片机-工控设备 - DSP/FPGA技术