3个变量表示的相图，图中，灰色平面为系统的Poincaré截面，图4(b)给出了在该Poincaré截面下系统的Poincaré映射。模式b为图3所示以点B为初始点，对系统进行积分，所得结果示于图5，同样图5(a)给出了相图，灰色平面为Poincaré截面，图5(b)给出了相应的Poincaré映射。
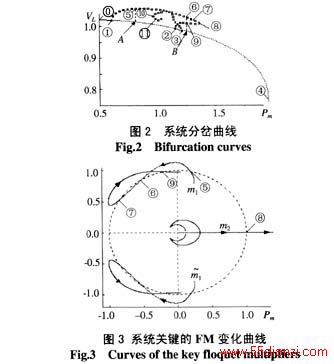
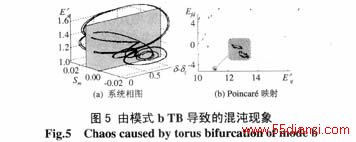
对比图4、5不难看出，由环面分岔TB导致系统出现的混沌现象，可能有2种不同的表现形式，由模式a导致的混沌现象一般表现为一个封闭的环面，其Poincaré映射一般为连续的环带；而由模式b导致的混沌现象往往表现为不规则的复杂图形，其Poincaré映射为不连续的环带。
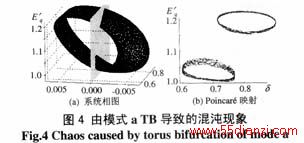
3.2 CTC的进一步分岔和自组织现象
同由连续PDB导致的混沌现象类似，CTC同样存在进一步分岔和自组织的现象。
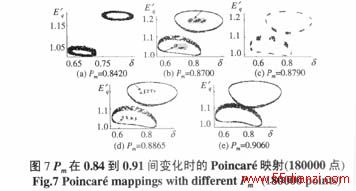
从系统平衡点附近开始，Pm取值0.8420、0.8700、0.8790、0.8865和0.9060，分别对系统进行积分，图6和图7给出相应的相图和Poincaré映射的情况，从它们的演化情况不难看出，系统中确实出现了自组织和进一步的分岔现象，前者可以使系统的混沌状态趋于有序，而后者则会使有序的状态重新回到混沌。
3.2 混沌子空间与有序子空间共存现象
在由环面分岔导致的混沌系统中，还存在仅某几个变量表现为混沌而其它变量为有序的现象，下面以例说明。
采用3.1节所用模型和参数, 并令TA=0.1, KA=100, Q1=0.1, Pm=0.6考虑如下2组初始值：① x0=[1.1400, 0, 1.0556, 2.3684, 1.1000, 1.0123]T, ② x0= [1.3000, 0, 1.0556, 2.3684, 1.2600, 1.0123]T,对系统分别进行积分，所得结果示于图8和9。实际上系统在失步点就已失去稳定(角度差大于2p)，图8和图9中失步点之后部分仅为说明系统的其它状态量并没有发散。
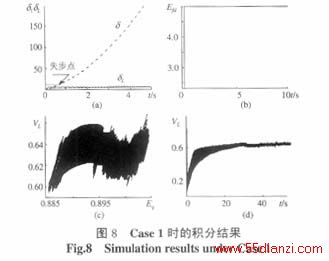
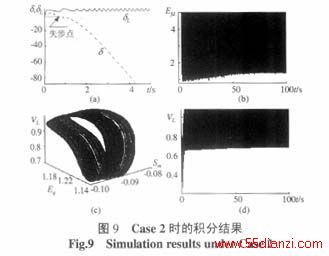
从图8和9可看出，由于初始取值的不同，系统的振荡形式也有很大的不同，但经过对数据的详细分析后发现，在2种场景下，系统中均存在混沌振荡，且均只表现在某些子空间上：对于 ① ，混沌子空间由E'q,VL,δL构成，而δ,sm,Efd子空间则是有序的，其中Efd为常数，而d 和sm为单调递增变量；对于 ② ，仅d 表现为单调递减变量，其它5个状态变量都处于混沌振荡之中。
在其它研究领域，同样发现混沌子空间与有序子空间共存的现象[14]，而在以往针对电力系统稳定和混沌现象的研究中，从未涉及此类现象，而它的存在，对解释电力系统为什么会出现纯电压失稳(某些节点电压幅值出现急剧变化，而运行角度变化较小)和纯角度失稳(单纯的角度发散而电压幅值变化较小)等现象会有帮助。但由于传统的关于混沌现象的定义已无法涵盖这类现象(传统的混沌系统要求满足有界性条件[1,13])，因而要研究此类现象，需要对传统的混沌定义进行必要的扩充。
4 结论
本文利用非线性动力系统分岔理论，研究了导致电力系统混沌出现的一种途径——TB现象，对由TB导致的混沌现象进行了全面的分析，并得出如下结论：
（1）因导致TB的弗罗奎特因子实部不同，由TB导致系统出现的混沌振荡表现为2种形式： ① 系统振荡分布在一个封闭的环面上； ② 复杂的扭曲环带，表明由TB导致出现的混沌现象非常复杂。
（2）以示例分析了具有环面特性混沌(CTC)系统的进一步分岔和自组织现象，表明CTC系统中存在着更深层次的动态分岔现象，需要进一步加以研究。
（3）以示例分析了在CTC系统中，有序子空间和混沌子空间并存的现象，它对于解释为什么电力系统中存在着不同的系统失稳模式有一定的帮助，但这类现象已经超出了传统混沌现象定义的范围，研究其规律需要对混沌现象定义本身加以扩充。
本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘
