1 引言
随着电力系统稳定问题的深入研究，国内外学者相继发现电力系统中存在十分复杂的混沌现象。混沌是非线性系统中各参数相互作用导致的一种非常复杂的现象[1]，它在电力系统中出现时，将伴随系统运行参数持续无规则的振荡，严重危害系统的运行安全。
Abed[2,3]和Srivastava[4]根据由连续倍周期分岔(PDB, Period Doubling Bifurcation)导致混沌的途径[5~10]及这一现象出现的规律，致力于研究消除电力系统混沌现象的办法。其后，在研究小扰动稳定域与混沌现象的关系中，又发现了由于初始能量直接激发导致混沌出现的途径[11]，但在实用的电力系统小扰动稳定域的研究中，可以不考虑混沌现象的存在[12]。
环面分岔(TB, Torus Bifurcation)也是导致非线性系统出现混沌现象的一种重要途径[1,13,14]，且具有环面特性的混沌系统具有许多奇特的现象，但在电力系统混沌现象的研究中却从未被论及，为此，本文借助一个简单的3节点系统[15]，对电力系统TB和经由TB出现的混沌现象的特点进行了分析。
用非线性微分方程表示的动态系统为
式中 x为状态变量，l为分岔变量。
平衡点方程为
f(x,λ)=0 (2)
静态分岔研究的是式(2)解的数目随分岔变量l连续变化发生改变而出现的分岔现象；动态分岔研究的是与式(1)的闭轨、同宿和异宿轨道以及不变环面的产生、消失和变化相关的分岔现象。
假设式(1)具有周期解，周期为T，当初始点为x0时，对应的解为xt = f (x0, t)，则有
定义1 (Poincaré截面)： 假设å是n维子空间U(ÌRn)中n-1维超平面，且满足 ① f(x)与å满足横截性条件，即f(x)×n(x)¹0，
xÎå，其中，n(x)为å在点x处的法线向量； ② å与受向量场f(x)控制的流f 相交于唯一点。则称超平面å构成向量场f(x)或流f的一个Poincaré截面。
定义2 (Poincaré映射)： 假设G为流f 的任意一条周期轨道，并与Poincaré截面å交于点p，由式(3)可得f(p, T)= p，即从p点出发的流，在一个周期的时间后，将回到p点。假设qÎU为p附近的一个点，当2点足够接近时，由q点出发的轨迹将再次与Poincaré截面å相交，定义对应轨迹第一次返回点的映射为：P:U®å，则对于任意这样的点qÎU，在映射P的作用下有
式中 t(q)为由点q出发的流返回å所需的时间。通常情况下，如果p¹q，则t(q)¹t(p)=T，但当p®q时，t(q)®t(p)。这里，将P:U®å称为流f的Poincaré映射。
定理1 (Floquet 定理)： 设f(x)由式(1)给定，f为向量场f决定的流，则有
式中 *代表一个(n-1)´(n-1)维矩阵，通常不为零。
定义3 (Floquet 因子FMs)： 定义f(x)的Poincaré映射雅可比矩阵DPp(p)的n-1个特征值为f(x)决定的流f的Floquet 因子FMs。
定理 2 设mi (i = 1, 2, ¼, n-1)为流f的n-1个FMs，若满足|mi|<1，i = 1, 2, ¼, n-1，则f 的任何周期轨道G都是渐进稳定的。
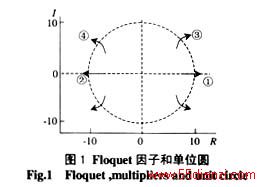
当系统参数l连续变动时，若有FM绝对值变为大于1，式(1)所示系统将出现动态分岔现象，稳定周期解被破坏。根据FMs变化的不同，可能遇到3类动态分岔现象：环面折叠分岔(CFB, Cyclic Fold Bifurcation)、倍周期分岔(PDB)和环面分岔(TB)，它们与非线性系统混沌现象的产生有着密切的联系，其中，① CFB：如图1中的①所示，有一个FM沿实轴从(1,0)穿出单位圆，将导致系统稳定的极限环破裂，周期轨迹发散。这同平衡点解曲线出现鞍节点(SNB)类似，只不过是SNB出现在系统稳定的极限环上； ② PDB：如图1中的 ② 所示，有一个FM沿实轴从(-1,0)穿出单位圆，这将导致系统周期解在此点处频率减半，周期加倍。当系统中不断出现PDB时，最终可能导致混沌现象产生； ③ TB：如图1中的③和 ④ 所示，有一对共轭的复FMs同时穿过单位圆，在这之后，系统的周期轨迹将出现圆环面振荡，即在近似正交的2个方向上出现周期不等的振荡运动，当2个周期不可约时，就可能导致系统出现混沌现象。在迭代系统中，TB又被称为内玛克分岔(Neimark Bifur-cation)[1,13]。
3 由环面分岔导致的混沌现象(CTC)
3.1 2种环面分岔模式
由图1可看出，当一对共轭的FMs穿出单位圆时，因其实部可正可负(见图中 ③ 和 ④ )，所导致的混沌现象也将不同。称导致TB发生的关键FMs的实部为正时称为模式a，反之为模式b。
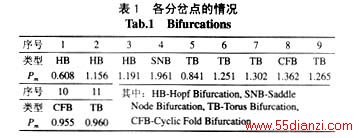
平衡点曲线和局部分岔点[1,13]，结果示于图2，表1给出了图2中各分岔点的情况。由图2、表1可看出，系统在Pm增大过程中先后出现了3次Hopf分岔(HB)，其分岔点分别为 ① 、 ② 和 ③ ，其中， ① 为超临界， ② 和 ③ 为亚临界。分别对由点 ① 、 ② 和 ③ 开始的极限环曲线进行跟踪[16]，可得到图2上部用实心方块(稳定极限环)和空心方块(不稳定极限环)表示的曲线，将曲线 ① ⑤ ⑥ ⑦ ⑧ ⑨ ② 发展过程中关键的Floquet因子(FMs)变化情况绘出并示于图3。由图3可清楚地看到，由于一对FMs 
的运动，导致系统出现4次环面分岔(TB)： ⑤ 、 ⑥ 、 ⑦ 和 ⑨ ，且 ⑤ 属于模式a，其它3个属于模式b。为研究模式a，以图2所示点A
本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘
