Lagrangian松弛法（LR）是求解水火电调度问题最成功的方法之一［1～3］。与其他方法相比，它能灵活处理多种约束［2］。LR方法的基本思想是用一组乘子松弛掉系统负载和备用约束，从而得到一个具有两层结构和可分性的优化问题。LR方法最突出的优点为计算量随问题规模的增大仅呈线性增长，因而节省时间［2］。且计算中得到的对偶信息可以用来衡量可行解的质量。
在标准LR方法框架下，解的震荡是一个严重的和固有的缺点。文［4，5］分别用增广LR法和非线性近似法解决由燃料费用函数线性引起的震荡并取得了良好的效果。除了这种震荡，实际中还有另一类更为严重的同构震荡，即当存在相同机组（机组参数完全一致）时，无论乘子如何修正，对应于相同机组子问题的解是完全相同的。这样将使求得的对偶解严重偏离最优解。到目前为止，还没有好的办法克服此种震荡。
文［6］直接用伪次梯度法求解水火电调度问题，但由于没有引入惩罚项，因此当低层求解几个相同机组子问题时，震荡会再次出现。文［7］用摄动法把相同机组的参数变为不同，虽减弱了震荡，但改变了原问题。且这些方法均无任何措施来降低对偶解对约束的违反程度。在文［4］中，由于增广松弛函数破坏了可分性，使惩罚项被线性化，这样一来，相同机组引起的震荡又会出现。实际上，只有用某种合理的方法把相同机组化为不相同，震荡才能克服。
引人惩罚项后，不能利用可分性在低层求解所有子问题以获得次梯度，并以它作为乘子的修正方向。本文结合文［8］中提出的伪次梯度法，用伪次梯度替代了次梯度作为修正乘子的方向：只求解一个或几个子问题并引入惩罚项，在惩罚项中把与其他机组有关的变量作为常量处理，即可获得伪次梯度。其优点是当求解了一个子问题后，如接着求解一个与它相同的子问题，则无论乘子是否改变，惩罚项中其他机组变量合起来作为常量处理的那一部分已经改变，从而形式上的“费用函数”已变得不同了，这就克服了震荡。引入惩罚项的另一优点是可以明显地降低对偶解对约束的违反程度，因此可对最后获得的可行解质量带来有利的影响。数值测试也表明了这一点。
2 同构震荡分析
费用函数Ci（xi（1），zi（1））定义为［6］
用标准LR方法求解式（1）时，低层会产生2个相同子问题：
无论乘子取值如何，离散变量zi（1）或全为0，或全为1，不会出现一个取0、一个取1的情况。这就远离了最优解。
根据文［9～11］中的对偶理论，高层求解的问题为
由图可见，在
附近解出现了震荡，无论乘子在式（7）中如何被更新，始终得不到原问题的最优解。
3 问题描述
考虑一有I个火电机组的电力系统，其调度目标是：在给定的时间范围T内决定各机组的启停及开启状态下的发电量，以使总燃料费用和启停费用最小并满足系统负载和备用的需求。 文中一些常用记号定义如下：
pi（t）为机组i在第t小时的发电量，MW；Ci（pi（t））为机组i在第t小时发电量为pi（t）时的燃料费用，；T为调度周期的总小时数；Pd（t）为第t小时系统负载需求，MW；Pr（t）为第t小时的系统备用需求，MW；xi（t）为机组i在第t小时的状态变量，记录目前机组已开（正整数）或已关（负整数）的小时数；ui（t）为机组i在第t小时的离散决策变量，取1表示下一小时机组开启或仍保持开，取－1表示下一小时机组关闭或仍保持关；Si（xi（t），ui（t））为机组i在第t小时的启停费用，
；ri（xi（t），pi（t））为机组i在第t小时能提供的备用，MW，如果xi（t）＜0，则ri（·）＝0。
引入上述记号后，水火电调度可描述为下述混合整数规划问题： 
单个机组的物理约束包括状态转移约束、发电量限制，某些机组可能还有爬升约束、最小开关机时间约束、首末开机时发电量最小约束等［2］。
4 算法描述
与文［2，5～7］中引入的松弛函数不同，定义式（9）的Lagrangian函数为
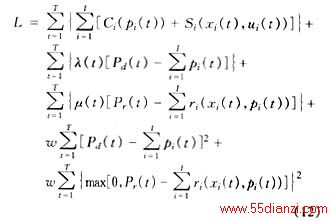
式中 λ（t）和μ（t）分别为第t小时的系统负载和备用约束的乘子；w＞0，是罚因子。
引入其他符号如下：
P和U是I×T矩阵，且Pit＝pi（t），Uit＝ui（t）。
当开、关机决策变量U给定后，所有的xi（t）就确定了，因此式（12）可改写为
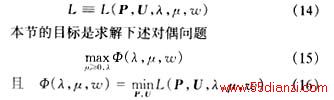
式（16）中，P和U满足所有单个机组的物理约束；当w＝0时是可分的，因而容易求出精确解。
记式（15）和式（9）的最优解和最优值分别为
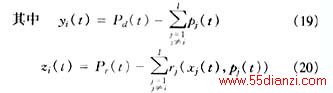
此时yi（t）和zi（t）是常量，且式（18）只涉及到机组i，故用文［2］中给出的方法很容易求解。至此，我们给出如下带惩罚项的伪次梯度算法Penalized Surrogate Subgradient Method（PSS）步骤：
（1）初始化
上述处理是为了保证算法收敛。定义伪次梯度为［6，8］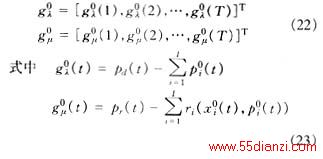
本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘
