具有相同机组水火电调度问题的新算法

    然后置迭代次数j＝0。
    （2）按下述公式修正乘子λ和μ


如未找到P^j＋1和U^j＋1，则置P^j＋1＝P^j、U^j＋1＝U^j。实际上，除第i行外，保持P^j和U^j的其他行不变并求解由式（17）定义的子问题（P－i）即可得到P^j＋1和U^j＋1。这些子问题可依次求解，然后计算新的伪次梯度

　　（5）用文［2］中的方法从对偶解出发构造可行解，停止。
　　在上述算法中，Φ^＊（w）并不能预先知道，实际使用时可用它的一个滑动估计^［2］，类似于文［8］，即可证明：算法的收敛性和对偶函数值（式（16））是原问题最优费用下界的性质。乘子的初始化可由优先分配表确定^［2］，但PSS方法对初值并不敏感。
　　以上算法与标准拉氏松弛法的最大区别在于：针对每次高层迭代或乘子更新，只有一个低层子问题求解。因此，虽然式（12）的惩罚项中存在不同编号机组的交叉项，但子问题之间仍然是可分解的。

5　数值测试

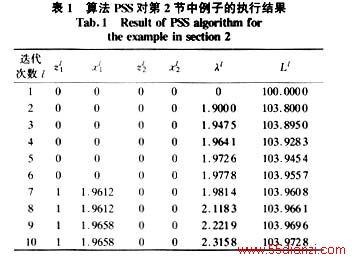
　　先将算法PSS用于第2节中的简单例子，算法的执行结果表明解的震荡可避免且可得到原问题的最优解。表1给出了该算法高层的若干次迭代结果，取罚因子为w＝25，第l步迭代步长α为0．95×（104－L^l）／（l×‖g^l‖²）。　　PSS算法的第2个算例是求解一个具有10台机组的短期调度问题，机组参数见文［6］。此例中，机组1、2是相同机组，机组3～8是相同机组，调度周期长为24 h。表2和图2对4种算法进行了比较，4种算法分别为：标准次梯度法Standard Subgradient Method（STS）^［2］；伪次梯度法Surrogate Subgradient Method（SUS）^［6，8］；参数摄动法Parameter Perturbation Method（PAP）^［7］；带惩罚项的伪次梯度法（PSS）。

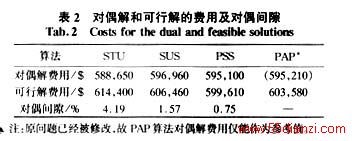
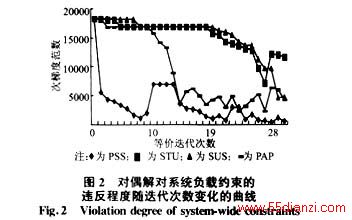
　　表2总结了各种方法得到的对偶解和可行解的费用及对偶间隙。用对偶间隙可以衡量可行解的质量，其间隙越小可行解的质量越好。从表2可看出无论是对偶间隙还是可行解的费用，PSS算法都是最小的。
　　为了进一步检验惩罚项的引入对相同机组解震荡的影响，算法最后得到的对偶解列于表3。表3只给出了PSS算法1～6h的结果，从中可看出相同机组的解不尽相同，因而克服了震荡。实际上PAP算法和SUS算法最后的对偶解也具有这个特点，STU算法却不具有此特点。衡量对偶解好坏的另一个指标为对偶解对系统负载约束的违反程度，用次梯度的范数表示。‖g_λ‖₁越小，越有可能得到好的可行解^{［2，5～7］}。图2描绘了4种算法执行过程中得到的对偶解对负载约束的违反程度随迭代次数变化的曲线。由于几种方法的迭代次数都比较大，对每种方法从第1次到最后一次迭代均匀取30次，仍能准确地反映违反程度的变化趋势。由此可见PSS算法的效果最好。

6　结论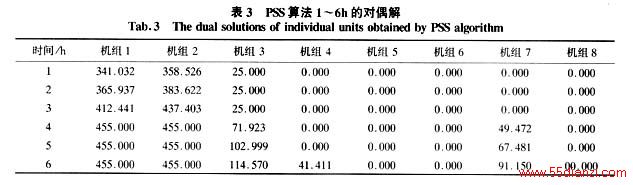

　　基于Lagrangian松弛的水火电调度算法的一个重要缺陷是当系统存在相同或相近子问题时，会产生严重的解震荡。本文通过对一个简单例子的分析，提出了一种新算法。通过引入二阶惩罚项并结合伪次梯度法，把相同子问题化为不同，从而克服了震荡，并显著地改善了可行解的质量。数值计算表明新算法十分有效。尽管测试例子是一个规模较小的问题，但所有分析是基于一般情况进行的，因此结论具有一般性。由于新算法在低层迭代时仅需求解一个子问题，所以，当问题规模增大时优势将更为明显。

上一页  [1] [2] 

本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘