串补输电线路的精确故障定位算法

摘  要：在具有串联电容器的输电系统中，由于具有非线性伏安特性的MOV （用于串补的过电压保护）的存在，使得常规的故障定位方法不能适用。文章提出了一种适用于串补输电线路的故障定位算法，计及了故障时串补及其保护装置的状态。算法利用两端不必同步的电压电流数据，分为两个子算法，分别假定故障位于串联电容器之前和串联电容器之后，最后通过比较不同序中的解，求出故障点的位置。仿真计算表明该算法对于不同的接地电阻和不同的故障类型有很高的精度。
    关键词：串补线路；故障定位；金属氧化物避雷器

1  引言

    电力系统中的故障大多数都是输电线路的故障。因而确保输电线路正常运行就成为非常紧迫的课题。故障位置的确定对电力系统的经济运行和电能的输送、质量都是极其重要的。永久性故障位置的确定有助于及时排除故障和恢复供电，瞬时性故障的精确定位对预防性维护有利。及时准确的故障定位可以减少维修时间，进而提高系统稳定性。

           串联补偿在长距离输电线路中广泛应用以提高线路传输容量，它还具有提高系统暂态稳定性，优化输电线路潮流和降低系统损耗的作用。串补电容器设计和应用中考虑到串补装置的过电压保护，普遍采用了具有非线性伏安特性的MOV。由于非线性MOV的存在，使得常规的故障定位方法不适用于串补系统。故障的发生造成MOV的动作，故障定位算法必须计及故障时串补及其保护装置的状态，才能实现准确的定位。

    目前有许多关于串补线路故障定位的研究。如通过估计得出串补上的电压降，将其用于串补系统故障定位和继电保护研究^[1]；使用两个子程序来分别计算串补前后的故障点，然后选择正确的结果^[2]。两者都使用了集中参数输电线路。以上都属于单端故障定位，利用单端数据的测距算法不受通信技术条件的限制，但原理上很难克服对侧系统运行方式对测距精度的影响。文[3]是基于双端故障定位，但是它的信号需要双端同步。而实际上，由于存在种种困难，信号的同步很难做到。

    本文参考文[4]、[5]，介绍一种精确故障定位算法，它不需要双端信号同步，对不同步信号进行了同步化处理，并且考虑了非线性MOV。本文中的定位算法包括两个子算法，分别用于计算电源到串补段的故障和串补到负载段的故障，这样得到两个预计的故障点。然后，通过一定的方法选择正确的结果。本文的算法同样可适用于同步算法。

 

2  串补模型

    串补的过电压保护对故障定位和串补线路保护有重要的影响。目前，各国大都采用MOV作为串补装置的主保护。

    图1给出了一个典型的串补装置的保护方案^[1] 。

当加在串补上的电压超过一定的电压水平V_ref, MOV开始作用。

 

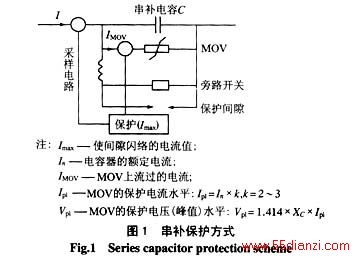
　  MOV的伏安特性可以用单指数或者多指数模型来模拟。单指数模型如下式                                                 

式中  I_max和V_pl的定义如图１。a一般为30~50。

    MOV吸收能量，通过过载保护防止MOV过热损坏。在MOV过热时，间隙闪络，旁路MOV。多指数模型则是将MOV的伏安特性曲线分段用不同的指数函数来表示。不在此详述。

    Goldworthy通过大量的算例计算，得到了一个可用于工频基波计算的串补电容器组和MOV组合模型^[6]。

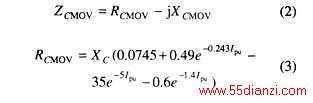
当 >0.98时，Z_CMOV满足上面的公式。则 、 。另外，当过载保护动作时，电容器旁路， 、 。本文中，考虑了串补电容器和MOV的组合模型。

3  算法介绍

    由于串补线路一般较长， 因而线路模型考虑了沿线分布的横向耦合电容，采用全分布线路模型。故障线路及其模型如图2所示。

                                  

　

    （1）子算法1：假定故障在送端——串补段

这里需要得到故障后线路送端M和串补一侧BC₁处的电压电流信号，通过受端N的电压电流信号，考虑串补装置的非线性特性，可以得到BC₁处的信号，然后可以利用一般方法（本文采用牛顿拉夫逊法求解）得到故障位置x₁。为了使信号同步化，引入首末端采样信号的相角差d。设输电

线路传递参数矩阵为，

x、l_C、l含义如图2所示，M、N端电压、电流分别记为U_M 、I_M 、U_N 、I_N ，BC₁、BC₂处与此相同，由M、N端电压电流推导得到的F点电压电流分别记为U_MF 、I_MF 、U_NF 、I_NF 。Z_C为串补装置阻抗矩阵。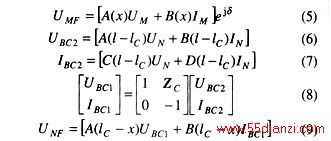
 

这里，有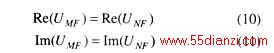 ，即它们的实部和虚部分别相等。

        

采用牛顿拉夫逊法解非线性方程组,即可求得x₁，d₁。

    （2）子算法2:  假定故障在串补——受端段采用与（1）相同的方法求取相应的x₂，d₂ 。

    （3）选取x的正解

    由前面两个子算法可以得到两组不同解，需要从中选取正解。如果x₁包含于 [0，l_C]，并且x₂不包含于 [l_C ，l]，则选取x₁作为正解。如果x₁不包含于 [0，l_C]，并且x₂包含于 [l_C ，l]，则选取x₂作为正解。对于算法中，存在同时满足x₁包含于 [0，l_C]，并且x₂包含于 [l_C ，l]的情况，求解中需要根据各序网中求得的解，比较得出正确的结果。

    由算法的原理可知，本算法同样适用于串补位于线路的首端或末端的情况，这种情况相当于本算法的一个特例，同时也可用于同步信号的处理。由于本算法考虑了串补/MOV组合模型，因而能够更确切地反映串补系统的实际情况。

4  算法验证

线路选取200 km长度的500 kV输电线路，串补位于线路的中点100 km处，补偿度为40%，计算时采用了不同的变换矩阵。计算结果如表1所示。

                          

　

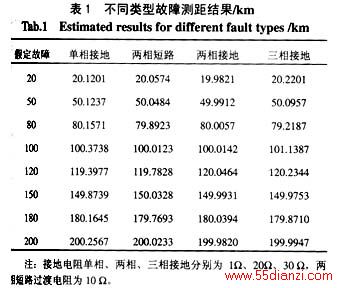
从计算结果可以看出，本算法具有较高的精度，对不同的接地电阻、故障类型同样适用。系统参数如下：

   

5  结论

    串补输电线路由于串补装置中非线性元件MOV的存在，使得串补系统故障定位与常规输电线路故障定位有较大差别，故障定位算法必须考虑到非线性MOV的存在。

    本文提出了一种适用于串补输电线路故障定位的精确算法。该算法的特点是：

    （1）考虑了串补装置中具有非线性特性的MOV，更确切地反映了串补系统的实际状况。

    （2）利用双端不必同步的电压电流数据，亦可用于同步数据。

    （3）数字仿真证明该算法具有高精度和很强的适应性，可满足不同接地电阻，不同故障类型的要求。

　

                            参考文献

[1] Novosel D，et al．Algorithms for locating faults on series compe-nsated lines using neural network and deterministic methods [J]．IEEE Trans．on PD，1996，11(4)：1728-1736．

[2] Saha M M，et al．new accurate fault locating algorithm for series compensated lines [J]．IEEE Trans．on PD，1999，14(3)：789-797．

[3] Sadeh J，Hadjsaid N，Ranjbar A M，et al．Accurate fault LOCAIION algorithm for series compensated transmission lines [J]．IEEE Tra-ns．on PD，2000，15(3)：1027-1033．

[4] Novosel D，et al. Unsynchronized two terminal fault LOCAIION estim-ation [J]．IEEE Trans．on PD，1996，11(1)：130-138．

[5] 束洪春，司大军，葛耀中，等(Shu Hongchun，Si Dajun，Ge Yaozhong，et al)．利用双端不同步数据的高压输电线路故障测距实用算法及其实现(Study on Practical Faule LOCAIION Algorithm for Two-Terminal HV and EHV Transmission Lines Using Asynchronous Data at Both Ends)[J]．电网技术(Power System Technology)，2000，24(2)：45-49．

[6] Goldsworthy D L．A linearized model for MOV-protected series cap-acitors [J]．IEEE PWRS，1987，2(4)：953-957．

本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘