任 震1,黄群古2,黄雯莹1
(1. 华南理工大学电力学院,广东省 广州市,510640;
2.中山电力工业局,广东省 中山市,528400)
摘 要:为了改善小波函数在电力系统故障信号分析中的性能,提高小波变换的运算速度,提出了新的小波函数构造方法及其相应的小波变换。该方法具有普遍性,所构造的小波具有简单、时频局部化性能好等优点。根据这种新的小波构造方法,提出了多层多分辨分析的快速算法。此外,利用多层多分辨分析的算法,对电力系统故障信号进行处理和分析,证明基于多层多分辨分析小波变换方法在检测电力系统故障时的突变信号分量方面,是一种非常有效的方法。该小波函数构造方法及其多层多分辨分析算法,同样适合于其它领域里的故障信号分析与信号处理。
关键词:小波变换;电力系统;多分辨分析
1 引言
在基于小波变换的理论及其应用研究中,小波函数的特性极为重要。小波变换的频率选择能力、它的局部化性能的好坏、以及由此所构造的
Haar小波函数及其相应的Haar小波变换,是最简单的正交小波函数和正交小波变换。用其对信号作小波变换时,高通分量具有差分性质,低通分量则具有算术平均性质。然而,由于Haar小波函数光滑性不够好,因而不利于对其作进一步的数学分析。此外,对某些信号进行Haar小波变换,所检测到的突变信息容易被误判为噪声信息。正因为如此,Haar小波函数的应用范围受到了一定的限制,一般用它进行理论说明[1]。
正整数N大于2的Daubechies小波函数在光滑性方面要优于Haar小波函数,但在时域局部化方面要低于Haar小波函数。
基于多分辨分析的Mallat算法是正交小波变换应用于工程实际的较好的小波快速算法。多分辨分析的中心思想是尺度函数的概念,它对空间不断划分,形成尺度函数以及由尺度函数构造的小波函数是多分辨分析的主要内容。此外,文献[2]建立了多小波变换的概念,即从建立小波函数矢量出发进行研究,这一点,与文献[3]不同。
有关小波函数的构造方法,可参阅相关文献[4],但本文提出的新的小波函数构造方法,所构造出的小波函数,在光滑性和时域局部性方面都较好,且其频域局部化性能较Haar小波函数也要相对高一些,但它们属于非正交小波函数类。
本文提出了多层多分辨分析,多层多分辨分析的层数N,从理论上讲,可为任意大于或等于2的正整数。当N为1时,多层多分辨分析退化为单层多分辨分析,所对应的算法即为Mallat算法。在这里,之所以出现N为1的情况,是因为所构造的新的小波函数退化为Haar小波函数。
2 新的小波函数的构造及特性
设支撑有限的(支撑为[-a/2,+a/2], a为实数)且对称的实函数s(t),它的傅立叶变换![]() (w)满足:
(w)满足:![]()
这样的实函数是容易找到的,例如对s(t)施行平移变换,得到两个子函数s1(t)和s2(t)。这里s1(t)= s(t-a/2)和s2(t)=s(t-3a/2)。由s1(t)和s2(t)定义的新的小波函数如下:

由式(2)、(3)、(4)可以得出新的小波函数及其变换具有下列性质(由于函数s(t)的特性使然):
(1) 新的小波函数的支撑是紧的;
(2) 新的小波函数满足容许性条件;
(3) 一般具有较好的频域局部性和光滑性。
本文根据以上的定义,构造出了下列几种时频性能较好的小波函数。
设a = 1,则有
(1)基于频域特性为三角形的小波函数为

![]()
还可以构造一大类相似的小波函数。
以上所构造的小波函数均类似于Shannon小波函数,因为Haar小波函数是由频域特性基本为矩形的函数构造的。
3 非正交小波变换的多层多分辨分析
从第2节新的小波函数的构造中可以看出,支撑有限的(支撑为[-a,+a],a为实数,一般取为1)且对称的实函数s(t)充当着尺度函数的作用。实际上,对上文构造的5种新的小波函数,构造它们的基函数(即三角形函数、梯形函数、余弦函数、升余弦函数和锯齿波函数)均可通过步长为0.5a的整数倍的平移变换所得到的函数类,构成L2(R)空间的基函数。因此,它们可以定义为相应于新的小波函数的尺度函数。
然而,上述5种尺度函数构成的函数类不是正交的,且当a不为2的整数倍时,由它们进行整数平移所组成的函数类不构成L2(R)的基函数(例如锯齿尺度函数)。但可以将它们划分为两类。
取a=1,则有:
凡是支撑为[N, N+1](N为整数)的函数类定义为第一类准尺度函数类。
凡是支撑为[N+0.5, N+1+0.5](N为整数)的函数类定义为第二类准尺度函数类。
:21.25pt;text-align:left; text-indent:-21.25pt;mso-layout-grid-align:none'> 第一类准尺度函数设为
第二类准尺度函数设为
{ψ2(2-jt+0.5) j,k∈z}
第一类准尺度函数类是相互正交的。第二类准尺度函数类也具有同样的性质。
下面根据上述第2节所构造的小波函数类型,对其相应的尺度函数进行分类。
(1)第一、第二类三角准尺度函数构成L2(R)的基函数。
(2)梯形准尺度函数类与三角准尺度函类数构成L2(R)的基函数。
(3)两类齿向相反的锯齿准尺度函数构成L2(R)的基函数。
(4)第一、第二类平方余弦准尺度函数构成L2(R)的基函数。
由第一类和第二类准尺度函数均可构造相应的小波函数。这样就把非正交的尺度函数划分为两个正交的准尺度函数。同样,对于通过步长为1/m(a=1)的整数倍的平移变换所得到的函数类,如果它们构成L2(R)空间的基函数,均可定义为尺度函数,并且可将该函数类划分为m类正交的准尺度函数,每一类都可以构造相应的小波函数。
上述非正交尺度函数分解为正交的准尺度函数的过程,或者由几个不同的准尺度函数组合成尺度空间的基函数的过程,就构成了多层多尺度分辨分析的主要内容。
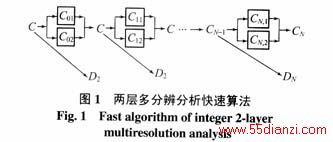
对于具有第一、第二两类准尺度函数的空间,可以构造两层多尺度分辨分析,其两层快速算法如图1所示。其中C01, C11, CN-1,1为第一类尺度函数的对前一级信号分解的低通部分 其中C02, C12, CN-1,2为第二类尺度函数的对前一级信号分解的低通部分。两类低通部分之和构成前一级信号在L2(R)空间的低通部分。其原理来自于上面导出的尺度空间V0是由它的两个准尺度空间(子尺度空间)V01和V02组成。同理,D1, D2, DN为第一类或第二类尺度函数的对前一级信号分解的高通部分。
从图1可以看出,当两类准尺度函数相等时,就退化为单一的正交的尺度函数,相应的两层快速算法就退化为一层的众所周知的Mallat金字塔算法。
对于整数M层多尺度分辩分析,其整数M层快速算法如图2所示。
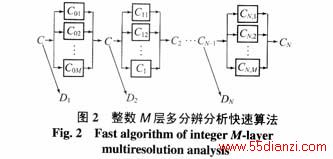
一般来说,应用多层多尺度分析进行信号分析与处理时,如果只要求提取信号的特征分量或其它奇异成分,则只要应用多层多尺度分析的任何一层就够了。从图2可见,这样的算法总共有M N种,如果考虑不完全分解的数目,则有N
4 基于多层多分辨分析的电力系统故障信号分析
电力系统故障时的突变信号一般具有4种类型[5],即有过零振荡(notching)、幅值隆起(swell)、幅值下降(sag)、局部跌落(dip)和瞬时断电(momentary interrution)
对这4种类型的故障信号,本章只就其中2种故障,即幅值隆起、幅值下降,使用第3节中介绍的第(2)类的梯形准尺度函数类与三角形准尺度函类数构成L2(R)的基函数,进行两层多分辨分析,以检测故障信号的特征信息。为了简便起见,本文对故障信号进行了2层分解,第1层是用梯形准尺度函数类进行分析,第2层是用三角形准尺度函数类进行分析,其变换结果如图3所示。
在图3中,显示了对电力系统信号发生幅值隆起故障(设为s1(t))时,对该信号进行2层多分辨分析的平滑部分和细节部分。图3(a)为第1层和第2层的平滑部分C01和C02,图3(b)为其细节部分D1。
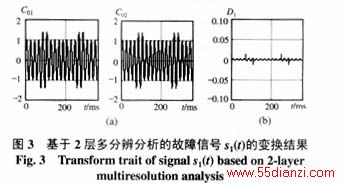
在图4中,显示了对电力系统信号发生幅值下降故障(设为s2(t))时,对该信号进行2层多分辨分析的平滑部分和细节部分。图4(a)为第1层和第2层的平滑部分C01和C02,图4(b)为其细节部分D1。
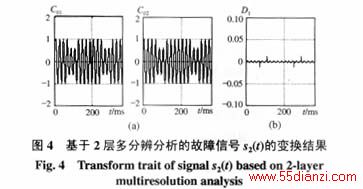
从图3和图4可以看出,基于多层多分辩分析的新的小波变换确实能快速地检测到故障特征。并且,由于新的小波函数的时域支撑为紧的,且又有较好的光滑性和局部性,因而易于对它作进一步的数学分析,并应用于许多工程实际中去。
5 结论
本文提出了新的小波函数构造方法及其相应的小波变换。该方法具有普遍性,所构造的小波具有简单、时频局部化性能好等优点。根据这种新的小波构造方法,本文提出了多层多分辩分析的快速算法。此外,本文利用多层多分辩分析的算法,对电力系统故障信号进行检测和分析,证明基于多层多分辩分析小波变换方法在检测电力系统故障时的突变信号分量方面,是一种非常有效的方法。
本文关键字:暂无联系方式电工文摘,电工技术 - 电工文摘