大规模发输电系统充裕度评估的蒙特卡罗仿

宋云亭，郭永基，程 林

（清华大学电机工程与应用电子技术系，北京100084）

    摘  要：针对模拟法在大规模发输电系统充裕度评估中计算量十分巨大这一难题，本文提出了基于序贯蒙特卡罗仿真的充裕度评估模型。模型中采用分层模型和合并相同状态技术显著减少了计算量，从而使充裕度评估达到了实用化水平。依据本文算法编制了相应的软件，并利用该软件对IEEE-RTS系统和总元件数达324个的实际大规模发输电合成系统进行了计算，计算结果表明，该方法正确有效，计算结果合理并具有实际应用参考价值。
    关键词：发输电系统；充裕度；蒙特卡罗仿真

1  前言
    发输电合成系统可靠性包括充裕度（Adequacy）和安全性（Security）两方面。充裕度是指发输电系统在系统内发、输、变电设施额定容量和电压波动容许限度内，考虑元件的计划和非计划停运以及运行约束条件下连续地向用户提供电力和电能量需求的能力。安全性是指发输电系统经受住突然扰动并不间断地向用户提供电力和电量的能力，突然扰动是指突然短路或失去非计划停运的系统元件。
    发输电系统可靠性评估的方法可分为两大类：解析法和模拟法。解析法主要是故障枚举法，当电力系统规模较小时，故障枚举法效果较好；当系统规模较大且要求考虑实际运行中复杂因素时，模拟法则更有效[1, 2]。
    对于大型发输电合成系统，需要模拟的元件很多，如发电机、变压器、输电线路、母线、断路器和继电保护等，还要考虑发电机组的检修安排和降额运行状态、负荷预测的不确定性和相关性、线路的共模故障和相关故障等，状态空间极为庞大，即使合并有关故障状态并简化发生概率较小的事件，所需研究的状态数仍然很多，采用解析法很难给出一个准确的数学模型，或者即便给出，也难以计算出准确结果。在这种情况下，概率模拟的方法更加适合，有时甚至是唯一可行的评估方法。因此在大型电力系统可靠性评估中，蒙特卡罗模拟法越来越受到国内外学者的关注[3-6]。
    本文提出了基于序贯蒙特卡罗仿真的充裕度评估算法，并将其应用于江苏田湾核电站外部电网的充裕度评估。
2  充裕度评估算法
2.1  蒙特卡罗仿真模型
    在蒙特卡罗模拟法中，首先要对系统内各个元件的状态抽样，其中，系统元件包括各种系统设备(如发电机、线路、变压器等)以及不同的负荷水平。
    对于电力系统中的任一元件k，设其强迫停运率为λk，Xk是它的运行状态，则Xk的概率函数P(Xk)为

    对于一包括m个元件的系统来说，Xi=(Xi1,Xi2,…,Xik,…,Xim)是系统运行状态的一个样本。根据各元件的强迫停运率和相互关系，可以确定其联合概率分布函数P(Xi)。例如当各元件的故障相互独立时

    从理论上来讲，对状态空间Ω中的所有状态进行抽样后，即可用下式计算系统可靠性指标的均值和方差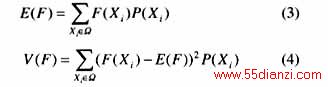

式中 F(Xi)是指示函数，代表第i次抽样中F(X)的观测值，可以是系统的停电标志（取0或1）或停电功率等。但在实际蒙特卡罗抽样计算中，由于实际抽样次数n一般远小于系统的状态数N，所以得到的只是E(F)和V(F)的估计值和，其中

式中 F(Xi)代表第i次抽样中F(X)的观测值。易于证明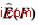，是E(F)的一个无偏估计，而与V(F)存在着下面的关系

2.2  减少计算量的方法
2.2.1  合并相同状态
    对系统的状态序列逐个进行评估时，如果状态中故障元件完全相同，计算出的切负荷量是完全相同的，而对可靠性指标的贡献只与该状态的持续时间有关，因此可以通过系统状态持续时间相加的方法将两状态进行合并。这里的相同故障元件包含：
    1）发电机本身或者是连接在同一母线上的额定容量、故障率、修复率均相同的不同发电机；
    2）线路本身或者是两端连接母线相同的线路参数、额定容量、故障率、修复率均相同的多回路线路；
    3）变压器本身或者变压器参数、变比、额定容量、故障率、修复率均相同的并联变压器。
    从元件状态持续时间抽样法的抽样原理可知，抽样产生的系统状态序列中包含许多相同系统状态，可以通过合并相同系统状态，采用存储系统状态和状态评估结果的方法来减少需要评估的系统状态数。
2.2.2  系统分层
    由于研究中我们对系统中各部分的关注程度是不同的，因此可以将系统分为A、B两层[7]：A层是我们所关注的主要部分，采用详细模型进行重点研究；B层为关注的次要部分，采用一般模型进行研究。B层与A层是有机联结的。
3  充裕度评估指标体系
    充裕度指标分为负荷点指标和系统指标两类，负荷点指标是对系统中的每个负荷点而言，表明故障的局部性影响，并可作为下一级系统可靠性评估的依据。系统指标则是全局性的，表明故障对整个系统的影响。系统指标包括基本指标和导出指标。下面的第1~6项为基本指标，包括概率、频率、持续时间和期望值四类；第7~9项为导出指标，是基本指标进行转换获得的，可以用于不同规模系统之间的比较。指标定义及计算公式如下：
    1）切负荷概率PPLC（Probability of Load Curtailments）

其中 S是有切负荷的系统状态集合；ti是系统状态i的持续时间，i是总模拟时间（本文中ti和T的单位为h）。
    2）年切负荷频率FEFLC（Expected Frequency of Load Curtailments）

其中Ni是有切负荷的状态数（如果系统状态序列中连续几个系统状态均有切负荷，将其视为一个有切负荷状态）。
    3）年切负荷持续时间TEDLC（Expected Duration of Load Curtailments）（h）

    4）每次切负荷持续时间TADLC（Average Du-ration of Load Curtailments）（h）

其中Ci是系统状态i的切负荷量。
    6）电量不足期望值EEENS（Expected Energy Not Supplied）（MWh）

    7）系统停电指标IBPII（Bulk Power Interruption Index），系统故障在各供电点引起的削减负荷的总和与系统最大负荷之比。它表明在一年中每兆瓦的负荷平均停电的兆瓦数，公式为

其中L是系统年最大负荷，单位MW。
    8）系统削减电量指标IBPECI（Bulk Power Energy Curtailment Index），一年中系统故障在供电点引起的削减电量的总和与系统年最大负荷之比（单位h）

        SSI表征发输电系统在最大负荷时全系统停电的年累计时间（单位min），是对系统故障的严重程度的一种度量。
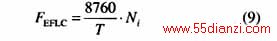
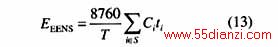
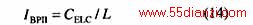
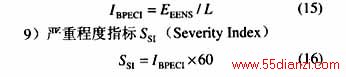
4  充裕度评估算法流程
    充裕度评估的目标是获得发输电系统各种可能出现的状态的概率和切负荷情况，然后统计可靠性指标。为了详细评估多重故障的影响，解决计算速度与精度的矛盾，一方面是要尽量减少需要评估的状态数，另一方面要尽量加速每一状态的评估速度。通过采用蒙特卡罗模拟法获得系统状态序列，并采用存储技术，合并相同系统状态和状态评估结果，极大地减少了需要评估的状态数。将多重故障评估转换为单重故障评估以加速评估速度，但需要保证在任意系统状态下单重故障的潮流计算均收敛且在采取适当的发电机功率调整和切负荷措施后无元件过负荷发生。充裕度评估流程如图1所示。

5  算例计算分析
5.1  计算条件
    根据前述评估模型和算法，对以江苏田湾核电站为中心的大规模发输电系统的充裕度进行了评估。
    田湾核电站外电网采用2005年主电网500kV及其所处L地区220kV网架；L地区的负荷等值到220kV变压器高压侧，其它地方的负荷等值到500kV变压器高压侧；发电机只考虑L地区高压为220kV和500kV的电厂中额定容量大于100MW的发电机组；线路上只考虑高压电抗器作为无功补偿设备，其它等值到负荷中。整个计算网络包括92个节点，129条线路，54台变压器，49台发电机。
5.2  系统分层模型
    对于本研究而言，我们主要关心系统的充裕度水平对田湾核电站的影响，故将外电网中与田湾核电站相连的J1、J2、J3节点及与这些节点相连的220kV网设为A层，电网其余部分设为B层。并对A层进行重点模拟。例系统主接线及分层示意图如图2所示。

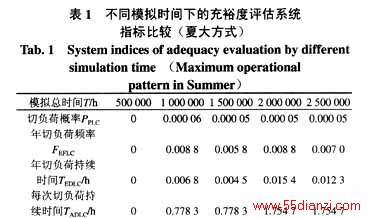
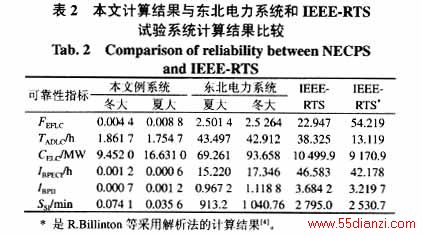
5.3  计算结果
    田湾核电站第一台1000 MW机组和第二台1000 MW机组将分别在2005年冬季和2006年夏季投入商业运行。考虑到系统将安排每台核电机组在冬季进行停堆检修和更换燃料，冬季有四个月时间只有一台核电机组运行，因此在计算中考虑了两种典型的运行方式：夏季大负荷方式（简称夏大方式）和冬季大负荷方式（简称冬大方式）。根据本文提出的算法，利用发输电合成系统充裕度评估软件TH-BESREP对田湾核电站外部电力系统进行可靠性充裕度评估。计算条件为：基于序贯仿真抽样的蒙特卡罗模拟法，交流潮流计算，采用年最大负荷单一负荷水平。计算环境是微机PII 400，WINOOWs 2000。
    夏大方式的计算结果如表1所示。系统状态抽样数与模拟总时间的增加成正比，因此可以用模拟总时间来表示系统状态抽样次数。

    从表1可以看出，在模拟总时间为50万小时下，各充裕度指标均为零，也就是说在所模拟的时段内未出现切负荷状态。原因是田湾核电站外部电力系统的充裕度水平较高，在较短的模拟时段内不会出现切负荷状态。
    改变模拟总时间为100万小时，此时将出现切负荷状态，进一步增加模拟总时间，各充裕度指标值将趋于稳定。但增加模拟总时间将同时加大计算量。模拟总时间为100万小时时，计算时间为2.21小时，而模拟总时间增加为250万小时时，计算时间则增加到5.23小时。为兼顾计算精度和计算量，本文取模拟总时间为200万小时的充裕度指标作为本研究最终的计算结果。
    本文例系统与东北电力系统和IEEE-RTS试验系统计算结果比较如表2所示。

    从表2可以看出，按照国际大电网会议（CIGRE）的指标划分方法，田湾外部电力系统的系统严重程度指标SSI应属于0级，为可接受的不可靠状态。而东北电力系统的系统严重程度指标SSI属于3级，为对用户有很严重冲击的不可靠状态。IEEE-RTS系统的系统严重程度指标SSI也属于3级。再综合表2的各项数据来看，可知田湾核电站外部电力系统的充裕度水平明显优于东北电力系统的可靠性水平，也高于IEEE-RTS系统的充裕度水平。
6  结论
    本文提出了基于蒙特卡罗模拟法的电力系统可靠性充裕度评估的算法模型，通过对IEEE标准可靠性测试系统和实际系统的计算，得到了相应的可靠性指标。结果表明，模型和算法是可行的，所编制的软件可用于实际大规模电力系统的充裕度评估。
    将软件应用于总元件数达324个的实际大规模发输电系统的充裕度评估，在计算中采用分层模型后显著缩短了计算时间，使充裕度评估方法达到了实用化水平。

参考文献

[1]   郭永基．可靠性工程原理[M]．北京：清华大学出版社，2002．
[2]   郭永基．电力系统新进展[M]．北京：冶金工业出版社，2000．
[3]   Guo Yongji，Xi yongjian，Xiao Kai et al．Composite system reliability evaluation based on Monte-Carlo simulation combined with outages screening[J]．IEEE Trans on PWRS，1999，14(2)：785-790．
[4]   Billinton R，Li Wenyuan．Reliability assessment of electric power systems using Monte-Carlo methods[M]．New York and London：Plenum Press，1994．
[5]   丁明，戴仁昶，刘亚成，等（Ding Ming，Dai Renchang，Liu Yacheng et al）．概率稳定性的蒙特卡罗仿真（Monte-Carlo simulation approach to probabilistic stability）[J]．清华大学学报（Journal of Tsinghua University），1999，39(3)：79-83．
[6]   鞠平，吴耕扬，李扬（Ju Ping，Wu Gengyang，Li Yang）．电力系统概率稳定的基本定理及算法（Fundamental theorems on probabilistic stability of power systems）[J]．中国电机工程学报（Proceedings of the CSEE），1991，11(6)：17-25．
[7]   宋云亭，郭永基，鲁宗相（Song Yunting，Guo Yongji，Lu Zongxiang）．改进的概率稳定评估方法及其应用（Improved algorithm of probabilistic stability evaluation and its application）[J]．电网技术（Power System Technology），2003，27(3)：23-27．

本文关键字：评估  蒙特卡罗  电工文摘，电工技术 - 电工文摘