1 引言
电力系统中,快速控制电压和增加系统功角振荡的阻尼是系统稳定的两类不同性质的问题[1-2],二者既有联系,又互相矛盾。解决这对矛盾,即:寻找一种控制手段,既能快速控制电压,又能增加系统功角振荡的阻尼,是电力系统控制的一大难题[3-4]。
电力电子的发展,使电力系统的无功控制装置由调相机、串联(或并联)电容、电感补偿,发展到静止无功补偿器SVC(Static Var Compensa-tor),为电力系统提供了新的强有力的可控工具。由于SVC具有突出的控制快速性,因此,深入研究SVC控制在改善电力系统功角稳定性中的作用具有重要意义。如何考虑电力系统的非线性特性,为SVC设计出性能优越的控制器是目前研究的重要课题[5]。正确认识SVC对电力系统快速电压控制和功角振荡阻尼特性的影响是本文要阐述的主要问题。
本文首先用直接反馈线性化DFL(Direct Feedback Linearization)控制理论[6-7],为SVC设计了电压型非线性控制器。讨论了SVC纯电压控制对电力系统同步转矩及阻尼转矩的不同影响,设计出了信号调制型SVC综合非线性控制器。最后,对输电线上装设了SVC的单机无穷大系统进行了数字仿真。
2 DFL理论简述
对于某一类可控的单输入非线性系统,假定其输入—输出方程消去中间变量后,可写成高阶微分方程形式[8]
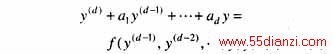
如果对于任意给定V,非线性微分方程
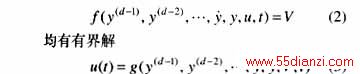
则对于系统式(1),施加形如式(3)的非线性反馈补偿后,原系统可化为全局线性化的新的受控对象

可把线性化后的系统运动方程式(4)化为状态方程
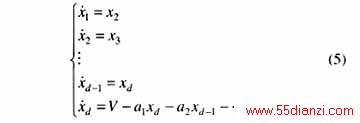
V是虚拟输入量,其控制规律可根据线性系统控制理论,针对线性化后的状态方程式(5)求得。
以上讨论的是单输入系统的情况,对于多输入非线性系统,其直接反馈线性化方法与单输入系统完全相同,参见文[6]。
实际系统有时是以状态方程描述的,在这种情况下,如果系统的相对次数等于系统阶数,则能够由状态方程求得如式(1)的输入-输出描述方程,从而可按上述方法使系统线性化;如果系统的相对次数小于系统阶数,也可用直接反馈线性化方法使系统的全部方程线性化,但此时所设计的控制器将出现输入量u的高阶导数,从而出现相应阶数的不能观测的隐动态(或零动态),引起复杂的动态过程,如果隐动态是不稳定的,其结果将导致DFL失效[9],在很多实际问题中该法难以实施。本文以下面控制器设计为例,介绍直接反馈线性化理论处理相对次数小于系统阶数情况的另一种方法,这种方法不以追求全部方程线性化为目标,而是从系统实际需要出发进行控制器设计。
直接反馈线性化方法不需要进行复杂的非线性坐标变换,因此,物理透明度高,比较简单、实用,便于工程界掌握。而且该法对于非仿射形非线性系统[10]及非光滑非线性系统均可适用。
3 电压型SVC非线性控制器设计
设简化的单机无穷大系统如图1,假定:
(1)发电机采用经典二阶模型,E¢恒定;
(2)发电机输入机械功率Pm恒定;
(3)把SVC和调节器的时滞统一考虑成一个一阶惯性环节[1]。
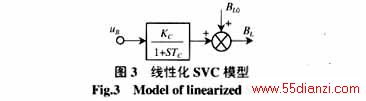
SVC框图如图2。


图中
![]()
a为可调电感的触发角;BLmax为可调电感的最大电纳值。
f
-1是f的反函数,这里起线性化作用。线性化后的SVC模型如图3。图中uB为要设计的SVC控制系统的输入信号;TC取0.1s。
在上述几个假定之下,具有SVC的单机无穷大系统的状态方程可写为
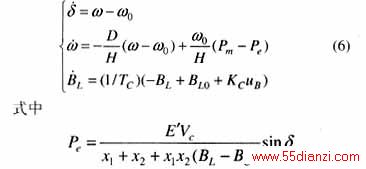
其中 d为发电机转子摇摆角(rad);w为发电机的转子角速度(rad/s);w