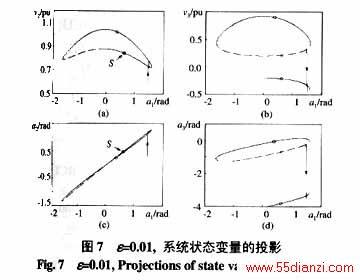
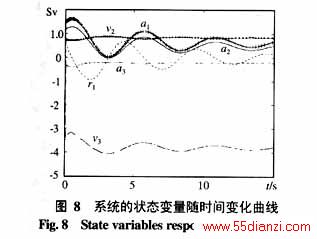
注2 由图7
4 ECUEP方法的改进
针对例1和例2,使用ECUEP方法及文[7]给出的概念性结构保持BCU方法分别进行暂态稳定分析,判定过程和结果比较如表1。
由表1可见,就本章给出的例子,文[7]给出的BCU方法能够与ECUEP方法获得相同的判定结果,但计算量却减少一半。而且,由于Controlling UEP方法的保守性,使用它在进行外部跳变判定时常常出现保守的误判。可知,故障后轨迹没有降落到Lh上,系统不稳定。而仅根据虚拟跳跃目标点判定,故障后系统应该是稳定的。从图中可以看出,对外部跳跃的方向作出判断是必要的。否则,仅考虑DAE系统的子模式x=f[x,h(x)]会引起故障后系统稳定性的误判。

根据文[15]中的定义2,BLE轨迹会在很短时间内逼近DAE的某一代数子流形,那么通过数值仿真,可以仅对BLE系统计算若干个步长便能够得到外部跳变方向及降落的代数子流形。如果假定仿真中不存在数值问题,那么,运用数值仿真的方法来判定外部跳变不仅可以克服Controlling UEP方法的保守性,而且也可以迅速地获得结果。对BLE系统的仿真目的在于:判定外部跳变行为时,只需仿真至能够获得结果便可停止,所以它与以前所说的用时域仿真方法来判定暂态稳定性是有区别的。
综上所述,对ECUEP方法进行改进,可引入数值计算方法来判定外部跳变行为。将改进后的ECUEP方法称为混合ECUEP方法(Hybrid ECUEP Method),其步骤如下:
(1)外部跳变行为的确定
以p为初值,对故障后DAE系统所对应的BLE系统进行数值仿真,并根据BLE轨迹来判定故障后系统是否外部跳变至Lh。如果跳变至Lh,则需要步骤2和3的进一步判定;如果不跳变至Lh,则判定故障后系统不稳定。
(2)临界能量的确定
1)由持续故障轨迹对应的虚拟持续故障跳变轨迹,找到DAE的Controlling UEPp0,co;
![]()
(3)稳定性判定

例3 对图1所示系统,考虑母线B2三相短路故障,且故障后系统与原系统保持一致。对于给定故障及实际故障轨迹末值,根据Hybrid ECUEP、ECUEP和文[7]给出的BCU方法,分别判断系统的暂态稳定性。
首先,使用Hybrid ECUEP方法进行暂态稳定判定。其步骤为:
(1) p=(1.25,0.50,0.29,0.75,-0.35,0.50),计算得到跳变降落代数子流形为Lh;
(2)此例使用与例1相同的系统,只是增大故障的持续时间,所以根据例1可知,![]() 18.1323;
18.1323;
