2）求取DAE系统的Controlling UEP。
尽管在Lh没有UEP，但是Lh边界是死巷点。故障后轨迹撞到死巷点仍然是危险的，运用文[16]提出的势能方法，用相关死巷点IS的能量函数值替代Controlling UEP，来作为DAE系统暂态稳定判定的临界能量。根据虚拟持续故障跳变轨迹可得相关的死巷点为(1.636,1.282,0.724, 0.003,0.433)。
（2）求取临界能量函数值
应用文[5],[16],[18],[21]定义的能量函数
则求取临界能量函数值的步骤为：
1）求取故障切除点及其对应虚拟跳跃点的能量函数值实际故障轨迹末值为p＝ (1.15,0.48,0.29,0.81, -0.33,0.53)，其对应的外部跳变目标点为q＝(1.15,0.48,0.84,0.89,0.15,0.74)，则E(p)=11.4710,E(q)=8.9735。
2）分别比较能量函数值
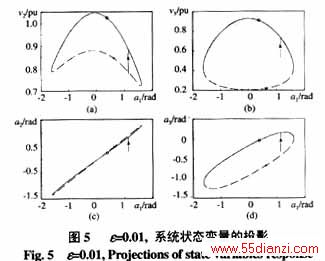
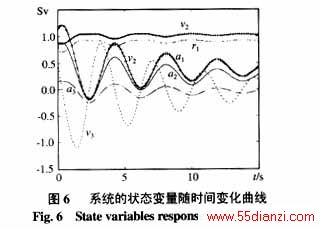
定，如图5、6所示。
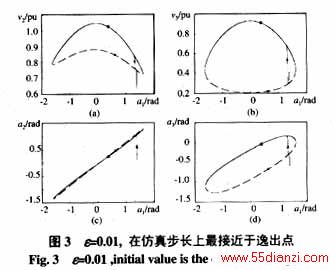
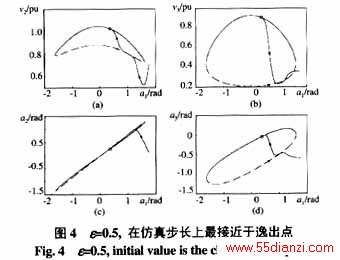
例2 对图1所示系统，考虑母线B2发生短路故障，且故障后系统与原系统保持一致。对于给定故障及实际故障轨迹末值，根据ECUEP方法，判断系统的暂态稳定性。
其步骤如下：
（1）同例1的步骤(1)。
（2）该步骤分两步，
1）实际故障轨迹末值为p=(1.48,0.56, 0.30,0.61, -0.40,0.37)，其对应的外部跳变目标点为q=(1.48,0.56,1.12,0.79,,0.14,0.59)，则E(q)= 14.8441,E(p)= 24.6886；
2）
但E(P)>Ecr，所以故障后系统不稳定，如图7、8所示。故障后轨迹趋于一不可运行的稳定平衡点(0.628,0,0.466,0.845,
