电力系统结构保持模型相关不稳定平衡点方法的判别算法研究

。

    引理

    其证明参见附录B。

其证明见附录C。
    虽然本文的讨论未涉及奇异面，但奇异面对暂态过程的影响是非常重要和复杂的^[5,6,16]。上述定理对暂态过程中由奇异面主导的电压失稳不能做出判定，因此, 为排除实际判定中奇异面的影响，可以通过计算代数方程雅克比矩阵的条件数方法来判定系统轨迹是否靠近奇异面，或运用文[16]提出的势能方法（Potential Energy Method）。下面，给出基于结构保持模型的ECUEP方法。
    扩展Controlling UEP方法（ECUEP）：设BLE系统的稳定域是局部严格等度连续的。
    （1）临界能量的确定步骤

    DAE系统的能量函数E_DAE(·)一般很难构造。因此在这里，它可以由能量函数E(·)作合理的替代。
    （2）稳定性判定步骤

）使用给定的持续故障轨迹和虚拟持续故障跳变轨迹, 计算故障清除时刻的能量函数值E(·)、E_DAE(·)。

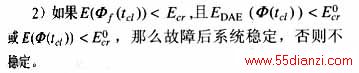
3.2  仿真算例
    考虑如图1所示的单机－两母线系统^[18]。系统的DAE模型如式(3)所示。其中,p₃=2,q₃=1。由于系统较为简单，由式(3)可以求得系统SEP附近的代数流形、UEP及死巷点（这些是本文所关心的），见图2。

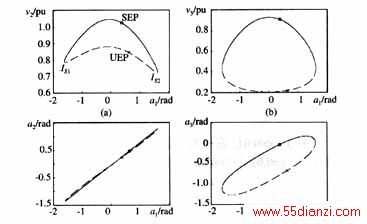
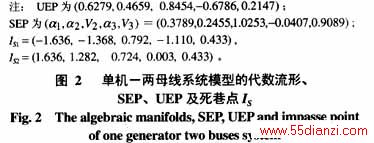
    例1  对图1所示系统，考虑母线B₂三相短路故障，且故障后系统与原系统保持一致。对于给定的故障及实际故障轨迹末值，根据ECUEP方法，判断系统的暂态稳定性步骤如下：
   （1）求取对应于BLE系统及DAE系统的Controlling UEP
    1） 求取BLE系统的Controlling UEP。
　　求取Controlling UEP一直是相关不稳定平衡点方法应用的障碍，BCU方法^[7,19]的提出使得这一问题得以较快速准确地解决。本文运用BCU方法解得BLE系统的Controlling UEP为(0.6279,0.4659,0.8454, -0.6786,0.2147)
    注1  运用文[7]给出的概念性结构保持BCU方法（Conceptual Network-Preserving BCU Method）及文[19]给出的方法计算Controlling UEP，当给定的e 很小时，BLE系统在数值上具有较强的病态特性，由持续故障轨迹从系统稳定域边界上的逸出点作为初值对故障后的降维系统进行积分，所得到的降维系统轨迹迅速趋于L_h附近，只有很弱的靠近Controlling UEP的趋势，如图3。如果将e 取大些，则故障后降维系统的轨迹在某一时刻较为趋于某UEP，如图4。而且随着e的增大，趋近程度越来越大，这样根据文

上一页  [1] [2] [3] [4]  下一页