就拿形式最简单的连接门电路的无源器件来说吧。上拉/下拉电阻可以将未用的数字输入设置为确定的逻辑电平(对于分立型CMOS来说这是绝对必须的)。开路漏极/集电极/发射极输出也需要上拉/下拉电阻以模拟方式设置数字电平。
但如何将门与无源器件组合在一起用作定时或平均组件让人更感兴趣。最基本的占空比至模拟电平转换可以用一个简单的RC滤波器实现,见图1。
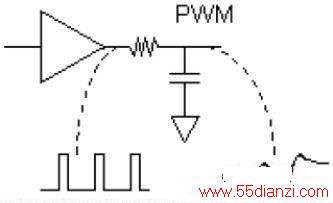
图1:将RC滤波器增加到一个逻辑门可以产生带纹波的电压值输出。
脉冲宽度调制(PWM)输出的是模拟直流电压值,这个电压值来自施加到RC滤波网络的连续高低逻辑电平之间的定时比例。从电容上的0V开始,每个连续的高电平都会使电容上的电压增加一点,直到经过大约5个RC时间常数后达到平衡。在平均过的直流电平上总是存在一个很小的纹波(图中有点夸张了)。为了得到最好的结果,脉冲频率要尽可能高,RC时间常数则尽可能长—与要求的稳定时间取得一致。
我们可以在最基本的数字类型的相位检测器中充分发挥这种效应(图2)。在锁相环中可以使用异或功能,因为经过RC滤波器滤波的输出电压直接正比于两个输入信号间的相位差导致的占空比。
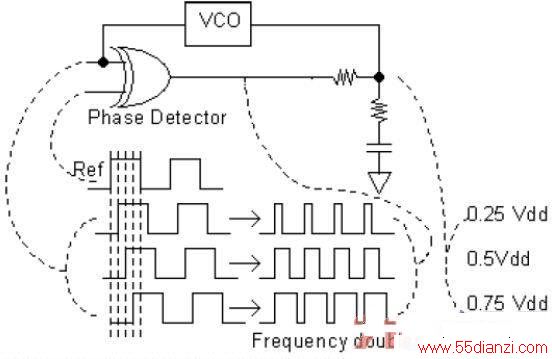
图2:一个异或门、一个压控振荡器和一些无源器件组成了一个倍频器。
将经过RC滤波器滤波的直流电平反馈到压控振荡器(VCO)可以将其频率锁定于参考频率。VCO输出和参考信号之间的这个相位差取决于VCO运行在与参考信号相同频率所需的电压值。
附带效果是异或相位检测器的频率翻倍功能。事实上,相同效应可以用于倍频器(图3)。
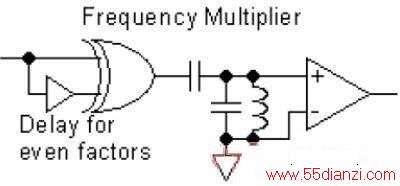
图3:利用一个异或门、一个运放、两个电容、一个电感和一个延时器实现的倍频器
异或门输出端的逻辑边沿使LC振荡器起振,这个LC振荡器被调谐为在想要的谐振频率发生谐振。当异或门输出端是一个对称的50%占空比时产生奇数谐振,偶数谐振可以用时延线剔除,这个时延线用于设置合适的异或输出脉冲占空比,以便最大限度地得到想要的谐振信号。放大器将LC振荡器的振荡恢复到数字逻辑电平值。
相位检测器、线路驱动器和脉冲整形器
如果真的希望参考信号和压控振荡器(VCO)之间的相位关系得到严格控制,我们可以看一些实例。在这种情况下,图2所示的XOR相位检测器并不能完全满足要求。例如当参考信号是一个随机的非归零(NRZ)数据流时,我们想要VCO进入相位锁定状态来产生恢复时钟,以便上升时钟沿发生在示波器上看到的数据眼图的正中。
由于接收器中的热噪声(及其它原因),弱信号的数据转换会适时发生“抖动”,因此采样数据以确定是1还是0的最佳时间是在最远离转换的时间点上——也就是模拟调制波形的幅度峰值处的眼中心位置。
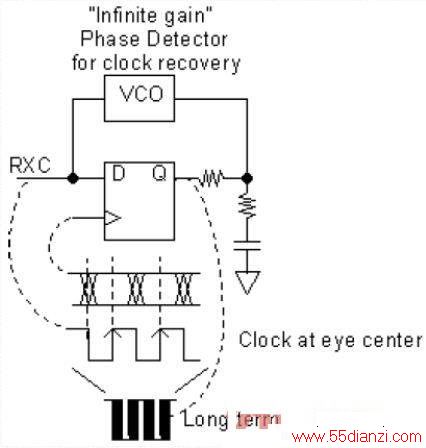
图4:D触发器和VCO可以让你将采样点设在信号眼图中心。
这里的输入数据流以时钟方式驱动D触发器,并在VCO时钟高或低的瞬间进行采样。(只有上升的数据沿进行时钟驱动。与延时输入进行异或可以同时实现上升/下降的数据沿时钟驱动,但没有必要。)平均后的直流输出反馈给VCO,直至VCO下降时钟沿找到数据转换。这样,真正采样数据位的上升时钟沿就处于它所属的眼图中心。这要求50%占空比的时钟,这样的时钟可以通过使用两倍于目标频率的VCO再进行二分频获得。
当数据流中存在很长的连续1和0时,最好是使用定时的三态泵上或泵下脉冲,除非RC时间常数可以做得与连续比特一样很长。
这是我所知道的唯一使用数字逻辑容忍D触发器找出自身亚稳态的一种方法,但不要紧,偶然的亚稳态结果只是在RC滤波器积分上千个脉冲期间的一点小瑕疵。
当然,所选择的D触发器的建立/保持时间必须要快,能够匹配数据比特率,但在整个建立/保持规范中会存在与温度和电源变化有关的漂移。“无限增益”这个名称有点不恰当。它的实际意思是,当D触发器工作在建立/保持时间违例场合,由于数据/时钟时序违例中有特别小的变化而导致触发器输出变高、变低或振荡。很奇怪,但确实是这样。
我最近一次使用这种技术是将74AHC74 D触发器用作相位检测器。最终的数字输出结果看起来类似于图4中的底部波形。如果能够在设计RC滤波器参数时更仔细些,我也许能够消除前后的频率波动,但老板是个急性子,要求我们赶快处理下一个紧急任务。不过对我们来说整个环路已经工作得足够好了。
用于补充数字输出的另外一个用例是推挽式(是的,我知道这是很老的术语)变压器驱动器(图5)。
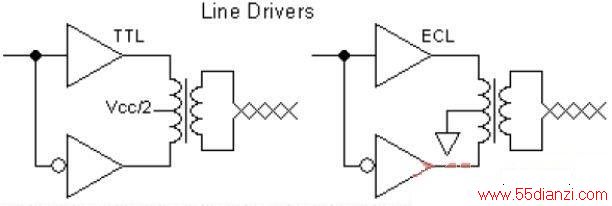
图5:变压器将逻辑门变成了线路驱动器。
中心抽头的VCC/2使得在逻辑高侧感应到的电压(由于逻辑低侧的下拉)不会因某些逻辑系列被二极管钳位到VCC 。我曾经用过这种技术,用的是74S系列TTL器件,中心抽头电压是VCC,并在原型中侥幸取得了成功,但我不推荐在产品化设计中使用这种技术。千万不要用74(A)HC来尝试,只能用ECL和74S TTL。如果是使用具有更强源驱动能力的AHC,中心抽头可以不要。
目前为止,所有这些无源器件都被应用到门输出端。下面是可以在门输入端可以做的一些事情,前提是它们是施密特触发器门(图6)。
读者可以浏览我的EDN设计思路“可配置逻辑门的施密特输入实现通用单稳态”了解有关这些设计的更多细节。
驱动谐振LC振荡器电路
现在让我们看看用逻辑门驱动谐振LC振荡器电路会发生什么事。图3已经对此有所涉及。下面让我们了解一下更多细节。图7给出了电路图。
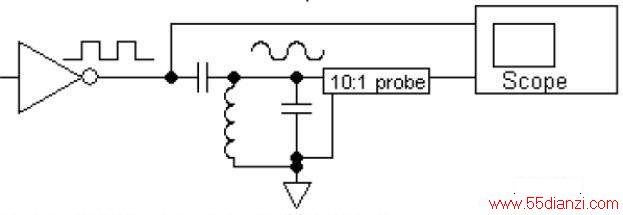
图7:振荡器谐振频率子谐波的一连串逻辑边沿将使振荡器起振。
图8显示了调谐在156.2kHz的振荡器对单个上升沿的响应。
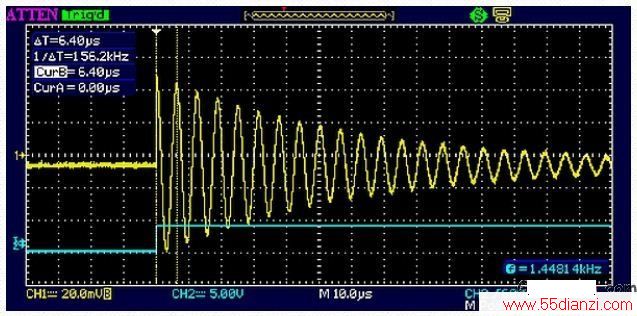
图8:单个蓝色边沿引发类似吉它弦的黄色振荡。(注意,下面所有图形都交换了颜色)
图7中的振荡器电路使用了一个可调(可调谐铁氧体块)的396nH电感并联一个1nF C0G(也叫NPO)电容,并通过一个68pF的电容松散耦合到TTL源。这个电路并没有使用镀铜板或PCB;所有元件放置在一个平台上,它们的引脚经空中焊接在一起。数据手册上标明的电感Q值在40MHz时大约为88,因此谐振频率为8MHz时的Q值(射频电阻/电抗)稍微有点高。电容比取决于电感Q值(一般来说电容Q值要比电感Q值好得多)、驱动器上升时间、想要的正弦波电平以及后面将正弦波过零点恢复到数字边沿的放大器增益。
在本例中,基于演示的目的,放大器用示波器表示,逻辑源是端接75Ω电缆和75Ω阻性负载的函数发生器的TTL输出。由于函数发生器的限制,实际占空比为48%,不是理想中的50%。
8MHz谐振频率来自公式f = 1/(2π&raDIC;LC)。但图9中的示波器显示器显示的触发黄色边沿信号频率为1.6MHz—是振荡器正弦波频率的五分之一。这个电路可以用作5倍频器,在实际应用中,到11阶或以上的奇数谐波需要根据电感Q获得(之所以提11阶是因为这是我曾经尝试获得的最高阶数)。
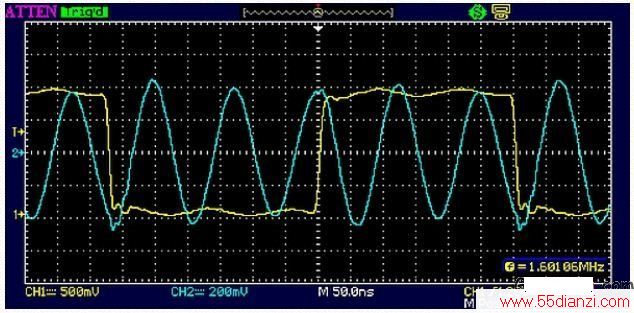
图9:一连串占空比约为50%的黄色边沿信号如果时序正确的话可形成连续的蓝色振荡波
在驱动沿和正弦峰值之间还存在其它相位关系。上升沿与正峰值相关,下降沿与负峰值相关。因此偶数谐波不能从50%的方波中剔除—不断变化的边沿将抵消相同极性的正弦峰(傅里叶先生是对的!)
本文关键字:暂无联系方式滤波-陷波电路,单元电路 - 滤波-陷波电路
上一篇:悬置带线带阻滤波器的设计方案