不过只要让边沿占空比稍作改变,我们就可以在偶数谐波处再次使正弦峰出现,比如图10中的6倍频器。
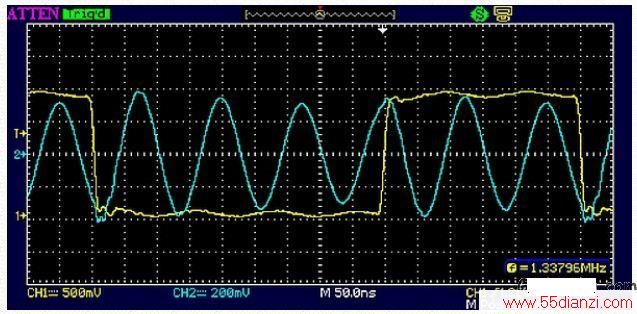
图10:出于演示的目的,这里用了一个40%占空比、1.333MHz的数字信号产生8MHz的6阶谐波,因为我不想重新调谐振荡器。
图11和图12显示了谐振倍频因子如何随占空比变化而变化。振荡频率在8MHz处仍然是常数,因为振荡器元件值没有改变,但现在矩形波频率分别位于8MHz的1/7分频(1.14MHz)和1/8分频(1MHz)。
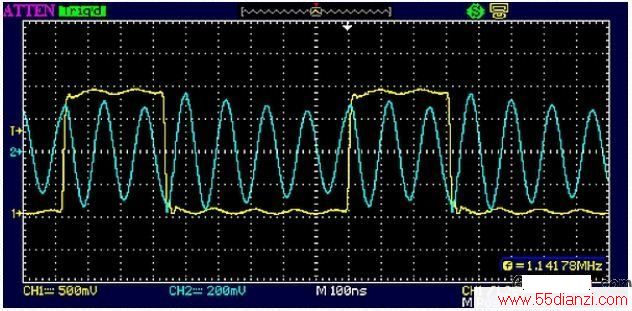
图11:35%占空比起振出1.14MHz矩形波的7阶谐波。
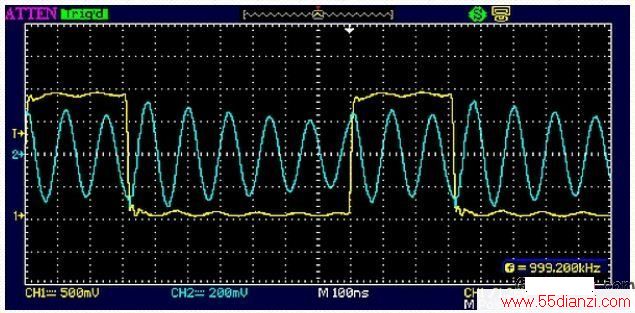
图12:31%占空比起振出1MHz矩形波的8阶谐波。
以此类推。只要不断改变的数字边沿能够落在最终正弦波的各个峰值处,振荡器就能起振。换句话说,交替变化的数字边沿之间的时间必须等于想要谐波的半周期的整数倍。
驱动脉冲长度
前面我们发现,驱动方波的占空比会影响其上升沿与下降沿和振荡电路峰值之间的关系(图7)。不过创建想要的脉冲长度是另外一回事,通常不是以数字方式完成的,它要求使用与我们试图重建的相同的高频时钟。
也许甚高频时钟和计数器链可以从我们想要倍频和合成目标脉冲的低频边沿触发。但也有模拟的方法(如前所述),它们使用单稳多谐振荡器、带门电路的RC网络以及使用现成集总LC与逻辑门器件的延时线或用于更高频的实际端接传输线。甚至可能使用一段不端接的传输线实现倍频,并使用反射脉冲的来回时间作为定时单元,但这种方法极富技巧。
下面我们来看一个有趣的例子,其中驱动脉冲是正弦波的半个周期或更短。由于函数发生器的限制,我不得不降低振荡器的谐振频率来获得想要的占空比。用于产生图13所示波形的振荡器电路使用了一个1μH的电感(Q值未知,实际上是废料箱中一个很小的射频扼流圈)并联一个100nF的电容,到数字驱动器的耦合电容必须增加到270pF。新振荡器的谐振频率大约是500kHz。函数发生器输出现在是主输出(非TTL),但上升时间缩短了,因为更快的TTL边沿引起了寄生振荡—也许是射频扼流圈的自谐振。
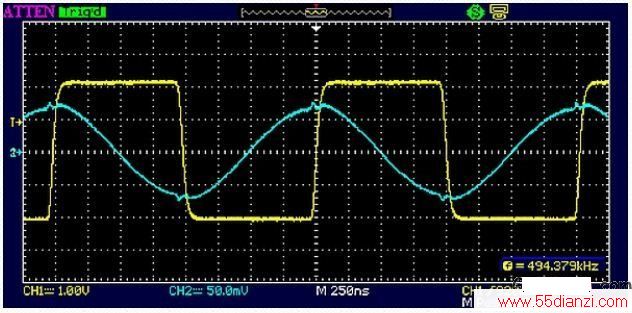
图13:50%占空比边沿与每个正弦波峰值对齐,脉冲边沿跨在正弦波的过零点。
那么将方波转换为相同频率的正弦波意义何在呢?其中之一是你可以消除振荡器带宽之外的高频抖动(Q值越高越好),特别是当从有噪声的串行位流中恢复位时钟时:
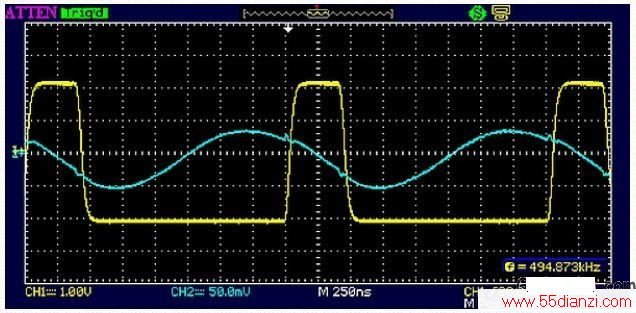
图14:在20%占空比时,脉冲边沿仍然跨正弦波零点。在这种情况下,脉冲宽度本身并不十分关键;利用宽松的定时方法(在合理范围内)创建脉冲宽度是可以接受的。
图15显示了一个驱动异或门的方波,它以窄脉冲(如图14所示)的方式在每个上升和下降沿驱动振荡器,但它很容易成为密集编码的串行位流,比如一个位有一个或两个边沿的双相或曼彻斯特位流。每个边沿触发振荡器输出双倍的位速率。恢复串行位时钟只需简单的除2方法。即使在一个位一个边沿的最小变换密度下,振荡器也会起振以填充丢失的边沿,并保持恢复时钟输出正常。我曾对4b5b编码的250Mbit/s串行数据使用过这种时钟恢复方法。

图15:异或史密特触发器可以很容易地使用简单的RC网络形成图3所示的稀疏脉冲。
这种方法比锁相环(PLL)加压控晶体振荡器(VCXO)要便宜得多,只要你不介意振荡器最初需要外力触发才能进入谐振状态的事实。它的工作量与调整吉它的六分之一相同。
适合数字逻辑振荡器的其它应用包括可变相移、串行位流采样时钟的自动相位校正、频率变换、分组时钟的启动以及将异或门用作混频器并通过频率加减法(外差法)实现的时钟合成。
本文关键字:暂无联系方式滤波-陷波电路,单元电路 - 滤波-陷波电路
上一篇:悬置带线带阻滤波器的设计方案