摘要：无功 功率计 量方法中的移相法有两种实现方法，一种是基于采样点平移，另一种是利用希尔伯特 滤波器 。在Matlab 上对这两种方法进行了设计、仿真，并采用 EP2C50 型号的 FPGA 实现了希尔伯特滤波器。数据表明基于采样点平移的方法有局限性， 而希尔伯特移相无功算法具有移相准确的特点，保证了无功功率的精确计量。
在电力系统运行时， 电网提供的能量有两部分： 一部分是有功功率， 用于能量单向转换； 一部分是无功功率， 用于 电路 内电场和 磁场 的能量交换。无功功率对外不做功， 但是对供电系统和负荷的正常运行十分重要，在电网中流动会引起电压和功率损耗。因此， 必须计量电力用户从电网吸收以及电网传送的无功功率的大小。
移相法是无功功率计量算法中的一种， 它是利用无功功率和有功功率之间的相位角相差π/2 关系， 用计算有功功率的乘法器来计算无功功率。
本文采用了两种方法来实现移相法， 在Matlab 上对这两种方法进行了设计、仿真， 并采用EP2C50 型号的 FPGA 实现了希尔伯特滤波器。
1 无功功率与有功功率的关系
假设电压、电流如式(1) 、式(2) 所示：
则有功功率、无功功率分别为：
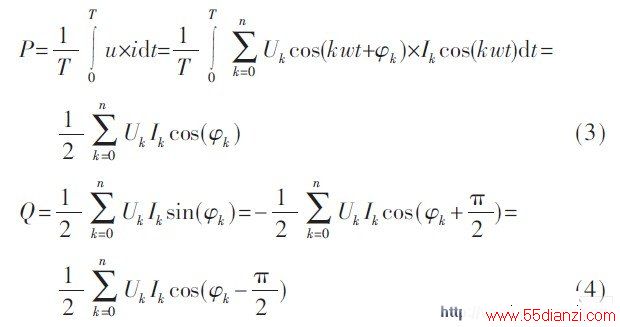
式(1)~ 式(4) 中，0~n 表示谐波次数，Uk 、Ik分别为电压电流幅值，φk为电压、电流的相位差； 式(3) 表示有功功率，式(4)表示无功功率。式(4)与式(3)相位角相差π/2 ，针对无功功率计算的移相法就是为了得到这π/2 相位差值， 这是利用移相法计算无功功率的理论依据， 即用计算有功功率的乘法器来计算无功功率， 这在数字信号处理中十分有用。在实际应用中，乘法器的两个输入序列变成移相后的电压序列与电流序列就可以实现无功功率计算。而在计算有功功率时已经获得了电压的采样值、电流的采样值及电压电流之间的相位角， 当采样点数满足计算谐波无功电能的奈奎斯特采样定理时， 针对计算无功功率， 有两种方法可以实现对离散信号的π/2移相： 一种是基于采样点平移来实现； 另一种则是通过Hilbert 变换来实现。
2 基于采样点平移的移相法
基于采样点平移的无功计量理论是将得到的离散的采样点信号进行π/2 移相( 若N 为信号一个周期内的采样点数， 则π/2 移相就是移动N/4 个点)， 然后采用式(3)计算无功功率。如图1 所示，曲线1 是原正弦波信号；曲线2 是基于采样点平移π/2 后的信号， 从图中可以看出，基于采样点平移的移相法精确地实现了π/2 移相。
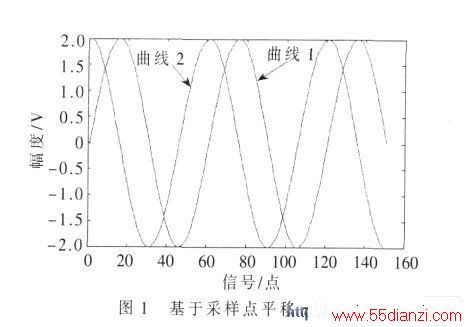
但是这种方法是针对基波频率的采样点移相， 实际应用时有其局限性。
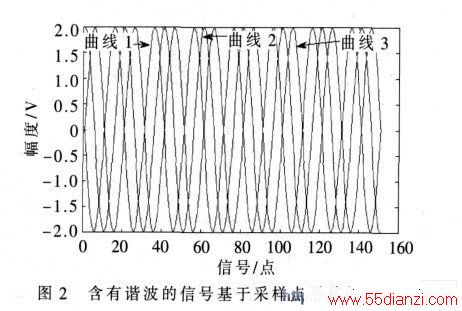
(1) 基于采样点平移方法要求被采样的信号只包含基波分量。假如对一个包含基波和3 次谐波的信号( 基波的每个周期2π 内) 进行100 次采样， 那么基波的π/2移相就是移动25 个采样点， 但是， 由于3 次谐波的周期缩为基波的1/3 ，25 个采样点对于3 次谐波而言， 已经是移相3π/2 了。如图2 所示， 曲线1 是原正弦波信号；曲线2 是理论上平移π/2 后的信号， 曲线3 是基于采样点平移后的信号， 实际已经平移了3π/2。
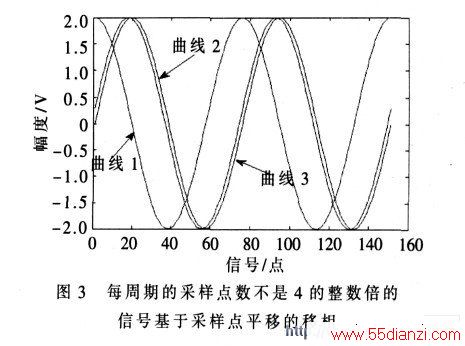
(2) 基于采样点平移还要求每个周期的采样点数是4 的整数倍， 否则将不能被4 整除而得不到π/2 的移相。如图3 所示， 曲线1 为原正弦波信号， 一个周期内采样点为75， 不是4 的整数倍； 曲线2 为理论移相π/2 的信号， 曲线3 为基于采样点平移的信号， 与曲线2 信号对比已有一定的偏移。
基于采样点平移的无功计量方法虽然存在其局限性， 但仍被一些要求不高的场合采用， 主要是其实现相对简单， 对硬件的性能要求也不是很高， 但是当电网中的谐波成分提高时，基于采样点平移计量无功电能的精度就很难保证。
3 Hilbert 变换计算无功功率
3.1 Hilbert 数字滤波器基本原理
理想的Hilbert 变换的定义为：
其幅值和相角分别为：
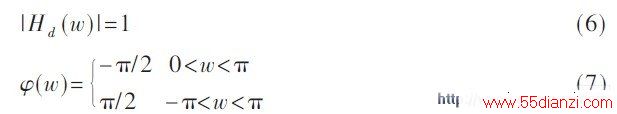
由式(6)~ 式(7) 可以看出，Hilbert 数字滤波器的幅值特性为1， 信号通过Hilbert 数字滤波器后， 其负频率成分进行相移π/2， 正频率成分进行相移-π/2。可见，Hilbert 数字滤波器能用于实现式(4) 计算无功功率。
3.2 F IR 型Hilbert 数字滤波器的Matlab 设计
线性相位FIR 数字滤波器的设计方法主要有窗函数法、频率抽样法和等波纹切比雪夫法( 即最优法) ， 本文采用等波纹切比雪夫法进行数字滤波器的设计。对于50 Hz 的工频基波信号， 若考虑最高谐波次数为19， 则可以将该数字滤波器所关心的频率范围设计为40 Hz~960 Hz。根据奈奎斯特采样定理， 采样频率Fs 应不小于2 倍的最高次谐波频率， 所以至少取2 kHz。
Hilbert 数字滤波器取N 为奇数， 设所要设计的滤波器的频率响应为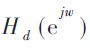
， 逼近加权函数为W(w)， 用线性相位FIR 数字滤波器的H(w) 做逼近函数， 则逼近误差函数为：
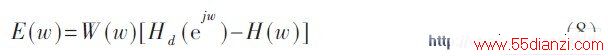
令δ=max{|E(w)|} ， 数字滤波器的设计问题就是寻找使δ最小的系统函数H(w)，即获取最优的单位冲激响应h(n)。所以数字滤波器应有式(9)所要求的频率响应：
图4 所示为等波纹切比雪夫法设计的Hilbert 数字滤波器的幅频特性和相频特性。从图中可以看出该数字滤波器具有良好的幅频特性和相频特性， 能获得严格线性相位及很好的衰减特性。
图5 为频率为150 Hz 的正弦波信号经过Hilbert 滤波器以后的信号。
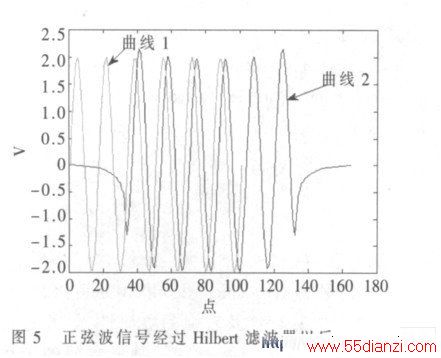
由仿真结果可知所设计的Hilbert 数字滤波器能精确地将所输入的电压谐波信号的基波及每次谐波都移相，并在此基础上计算获得精确的无功功率值。
3.3 FIR 型Hilbert 数字滤波器的FPGA 实现
3.3.1 FIR IP 核的生成
ALTEra 公司提供的FIR IP 核是一个高性能、参数化的IP 核， 可以用来实现FIR 滤波器。该IP 核支持全并行结构、全串行结构、多位串行结构、可变的多时钟结构等多种结构， 滤波器的参数可以通过该IP 核的参数化界面进行设计，也可以将在第三方软件中设计好的滤波器系数导入该IP 核中从而完成滤波器设计， 它的所有输入输出信号格式都与Aval ON 总线 的 ST reaming 结构的 接口 相符，可以方便地加入到应用工程中。
本文中FIR 滤波器的实现方法是将Matlab 产生的滤波器系数导入QUARTus ii 中的FIR IP CORE 中。图6是Quartus 生成的FIR IP 核。
3.3.2 FIR IP 核的的验证
由于所设计的Hilbert 滤波器的频率范围为40 Hz~960 Hz， 所以验证时将用频率为150 Hz 正弦波信号通过所设计的滤波器， 观察结果来验证该滤波器是否实现了π/2 移相。
本文讨论了无功功率与有功功率之间的关系， 以及计算无功功率方法中移相法的两种方法， 根据在Matlab中对基于采样点平移的移相法和Hilbert 滤波器法的仿真可以看出， 基于采样点平移的移相法在实际应用中有局限性， 只能在一些要求不高的场合采用。而Hilbert 滤波器法可以做到移相准确、计量精度高， 因此， 基于Hilbert 变换的移相算法是无功计量中较好的方法。
本文关键字：暂无联系方式DSP/FPGA技术，单片机-工控设备 - DSP/FPGA技术
