西门子PID调节应用及技巧探讨 .
点击数:7216 次 录入时间:03-04 11:41:52 整理:http://www.55dianzi.com 西门子plc应用
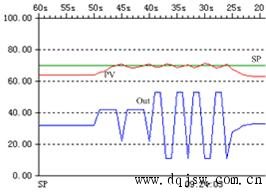 下面是整定得到的参数的曲线:
下面是整定得到的参数的曲线: 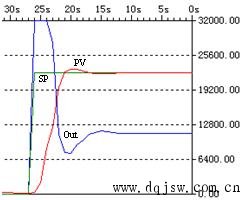 下面是另一组整定前的参数的曲线,过程变量PV曲线上升太慢:
下面是另一组整定前的参数的曲线,过程变量PV曲线上升太慢: 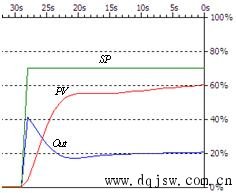 虽然整定前两组PID参数相差很远,两次整定后得到PID参数差不多,使用整定得到的PID参数的曲线形状也差不多。 我觉得西门子的PID参数自整定是很好用的。要用好PID调节,搞清楚PID的计算公式和PID参数的意义是很有必要的。下面是PID的公式:
虽然整定前两组PID参数相差很远,两次整定后得到PID参数差不多,使用整定得到的PID参数的曲线形状也差不多。 我觉得西门子的PID参数自整定是很好用的。要用好PID调节,搞清楚PID的计算公式和PID参数的意义是很有必要的。下面是PID的公式: 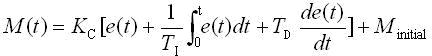 式中误差信号e(t) = SP(t) – PV(t),M(t)是PID控制器的输出值,Kc是控制器的增益(比例系数),Ti和Td分别是积分时间和微分时间,Minitial是M(t)的初始值,实际上是积分的初始值。 PID公式的前3项分别与误差、误差的积分和误差的导数成正比。 微分、积分是高等数学的概念,建议没有学过高等数学的网友至少要搞清楚微分和积分的几何意义,这对深入理解PID参数的意义有很大的帮助。 积分对应于下图中误差曲线e(t) 与坐标轴包围的面积(图中的灰色部分)。PID程序是周期性执行的,执行PID程序的时间间隔为Ts(即PID控制的采样周期)。我们只能使用连续的误差曲线上间隔时间为Ts的一些离散的点的值来计算积分,因此不可能计算出准确的积分值,只能对积分作近似计算。 一般用下图中的矩形面积之和来近似精确积分。当Ts较小时,积分的误差不大。
式中误差信号e(t) = SP(t) – PV(t),M(t)是PID控制器的输出值,Kc是控制器的增益(比例系数),Ti和Td分别是积分时间和微分时间,Minitial是M(t)的初始值,实际上是积分的初始值。 PID公式的前3项分别与误差、误差的积分和误差的导数成正比。 微分、积分是高等数学的概念,建议没有学过高等数学的网友至少要搞清楚微分和积分的几何意义,这对深入理解PID参数的意义有很大的帮助。 积分对应于下图中误差曲线e(t) 与坐标轴包围的面积(图中的灰色部分)。PID程序是周期性执行的,执行PID程序的时间间隔为Ts(即PID控制的采样周期)。我们只能使用连续的误差曲线上间隔时间为Ts的一些离散的点的值来计算积分,因此不可能计算出准确的积分值,只能对积分作近似计算。 一般用下图中的矩形面积之和来近似精确积分。当Ts较小时,积分的误差不大。 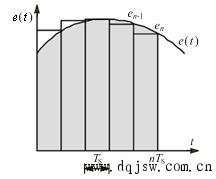 在误差曲线e(t)上作一条切线(见下图),该切线与x轴正方向的夹角α的正切值tgα即为该点处误差的一阶导数de(t)/dt。PID控制器输出表达式中的导数用下式来近似: de(t)/ dt ≈ Δe(t)/Δt = [e(n) - e(n-1)]/Ts,式中e(n)是第n次采样时的误差值,e(n-1)是第n-1次采样时的误差值。
在误差曲线e(t)上作一条切线(见下图),该切线与x轴正方向的夹角α的正切值tgα即为该点处误差的一阶导数de(t)/dt。PID控制器输出表达式中的导数用下式来近似: de(t)/ dt ≈ Δe(t)/Δt = [e(n) - e(n-1)]/Ts,式中e(n)是第n次采样时的误差值,e(n-1)是第n-1次采样时的误差值。 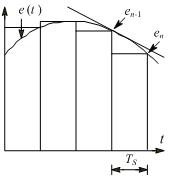 1.模糊控制的关键点在于总结大量的实践数据,然后做成黑匣子,看似神秘,实际都是经验参数!
1.模糊控制的关键点在于总结大量的实践数据,然后做成黑匣子,看似神秘,实际都是经验参数!上一页 [1] [2] [3] [4] 下一页
本文关键字:技巧 西门子 西门子plc应用,plc技术 - plc应用 - 西门子plc应用




