从式(15)可以看出,保证开关管实现ZVS的最小电流可由式(16)得到。
=n2VH
(16)
不同的吸持电容Ch数值与最大电压值VH所对应的ZVS范围如图4所示。开关管超前臂的关断损耗可通过给IGBT增加外接缓冲电容来减小。从图4还可以看出大电容Ceq对ZVS范围的限制。因此,Ceq的选择应综合考虑ZVS范围和超前臂的开关关断损耗。
2.2 滞后臂的ZCS条件
吸持电容的归一化值如式(17)所示。
Chn=(17)
图5所示为吸持电容不同归一化值所对应的原边电流的复位情况。为了实现滞后臂的ZCS,Ch的能量应该足够大,从而通过Lr使原边电流复位,且原边电流应当在滞后臂关断之前减小到
图5不同归一化Ch值对应的原边电流的复位零。从式(11)、式(12)、式(15)、式(16)、式(17)可得到式(18)。
arcsin
(1-D)(18)
从式(18)和图5可以看出,为了确保ZCS,应当增加Ch或VH的值。但是,VH的最大值不能高于输入电压反射到次级的电压Vs/n;同样,大电容Ch增大了环路电流,而环路电流又通过Ch间接加到了负载。综合考虑,软开关在变换器功耗方面的效果不仅与开关损耗的减小有关,还与由软开关引起的附加导通损耗有关。为了获得预期的效率,要求在设计时Ch的值取得越小越好,从而使附加导通损耗最小化。
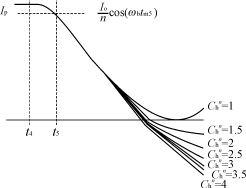
图5 不同归一化Ch值对应的原边电流的复位
2.3 输出耦合电感
为了保证辅助电路二极管Dc的软变换,输出耦合电感的漏感Llks应当满足式(19)。
Llks<(19)
式中:Dmin为最小占空比。
给Ch充电的谐振电流也耦合到了输出电感电流中,从而增加了输出电容的电流纹波。因此,Llks应当在满足式(19)的条件下尽量取大,以减小谐波电流的有效值。
3 实验结果
为了验证ZVZCS PWM全桥变换器的工作原理和性能,在实验室完成了一台80V/50A,80kHz的样机,其电路如图6所示,参数如下:
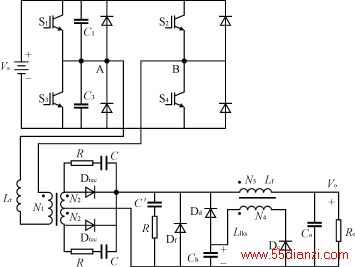
图6 样机电路原理图
输入直流电压Vs=630(1±10%)V;
输出直流电压Vo=80V;
变压器原副边匝比N1∶N2=5.33,变压器原边漏感Lr=9μH;
输出滤波电容Co=10000μF(电解电容);
输出滤波电感Lf=20μH,N3∶N4=1.12,漏感Llks=1.8μH;
开关管S1~S4(IGBT) IRGPH50KK2(1200V,30A);
输出整流二极管Dc,Dd,Df,Drec C60P40FE(400V,60A);
C1=C3=1nF;
Ch=0.47μF(电解电容);
R=30Ω,C=2.2nF,C′=6.6nF;
开关频率f=80kHz。
图7给出了实验波形。从图7(a)可以看出,在谐振周期内,原边电流减小到零,从而消除了原边的拖尾电流。从图7(c)可以看出,通过S4的电流在驱动脉冲下降为零之前已经减小到零,从而S4实现零电流关断。从图7(d)可以看出,在死区时间内,S1的电压减小到零,从而S1实现零电压导通。从图7(e)和(f)可以看出,在一个谐振周期内,Ch在满载时完全放电,而在轻载时却没有完全放电,使得环路电流根据负载条件变化作适应性调整。
图8给出了根据原理样机得到的效率曲线。满载时效率最高,达到94%。
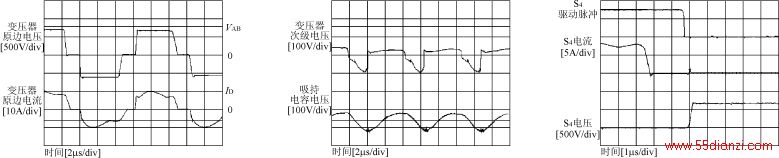
(a) 变压器原边电压和电流的波形
(b) 变压器次级电压和吸持电容电压波形
(c) 滞后臂S4的零电流关断波形
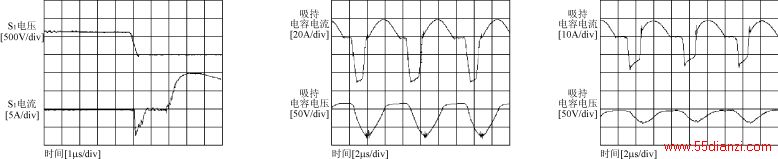
(d) 超前臂S1的零电压导通波形
(e) 满载时吸持电容上的电压电流波形
(f) 25%负载时吸持电容上的电压电流波形
图7 实验波形
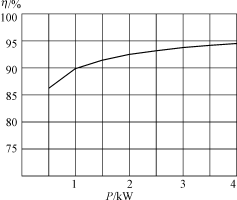
图8 原理样机效率曲线
4 结语
本文提出了一种新颖的ZVZCS PWM全桥变换器,并具体分析了它的工作原理、电路设计及性能。最后通过一台4kW的原理样机的试验结果,证明了该变换器具有以下主要优点:
——所采用的辅助电路无有源开关;
——次级整流二极管具有与传统的全桥PWM变换器相同的电压应力值;
——对吸持电容充放电的环路电流可根据负载的变化进行自适应调整;
——辅助电路二极管Dc实现了软变换;
——能够使变换器在开关频率为80kHz且满载时效率高达94%。
本文关键字:暂无联系方式电工文摘,电工技术 - 电工文摘