2 光伏矩阵数学模型
光伏电池I-V特性与太阳辐射强度S和光伏电池温度T有极大关系,即I=f(U,S,T)。采用单结晶硅为材料的光伏电池电路原理如图1 所示[6]。

Rsh为考虑载流子产生与复合以及沿电池边缘的表面漏电流而设计的等效并联电阻,Rs为扩散顶区的表面电阻、电池体电阻及上下电极之间的欧姆电阻等复合得到的等效串联电阻。
图1的太阳能光伏电池等效电路得出: I = IL- ID - Ish (1)
其中:I是光伏模块输出电流;IL是光生电流;ID是流过二极管电流;Ish是光伏模块漏电流。
根据电子学理论,由材料物理特性决定的理想二极管太阳能电池I-V特性为:

(2)

(3)
式中 V——光伏模块输出电压;ID0——二极管反相饱和电流;q——电荷电量;n——二极管性能指数;k——波兹曼常数;TC——太阳能电池温度;T0——绝对零度;T——外界温度。
当太阳电池处于开路状态时,开路电压
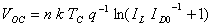
(4)
由公式(1) ~ (4) 得:
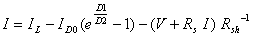
(5)
其中
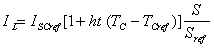
:
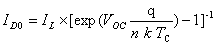
;
式中 ISCref——参考日照、温度下的短路电流;ht——太阳电池模块温度系数;TCref——参考条件下的基准温度;Sref——参考条件下的光照强度。
在一定的参数范围内,理想光伏电池等效串联电阻Rs很小,等效并联电阻Rsh很大,一般工程应用中可忽略不计[7],公式(5)简化成:
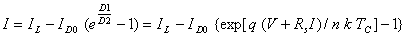
(6)
综合上述推导过程,光伏阵列的数学模型(6)反应出光伏电池受温度影响,和光照强度成正比,输入电流和输出电压之间呈现明显的非线性特性,因此可以用该模型模拟外界条件变化对光伏电池特性的影响,能准确反应物理特性,具有较高的仿真精度。
3 光伏矩阵最大功率跟踪数学模型
将Vmax代入公式(6)得Imax,于是最大功率Pmax可由下式求得: (10)
4 光伏矩阵仿真通用模型及应用
根据公式(6)~(10)考虑MPPT仿真算法,利用PSIM软件仿真功能设计光伏阵列通用仿真模块。图2是光伏阵列仿真模型内部结构,其中光伏矩阵模型和实时迭代MPPT算法均为PSIM提供的DLL控件采用C编程,实时求解任意太阳辐射、环境温度下对应的最大功率点电压、电流值。算法编写过程设置Switch,系统根据是否带有MPPT输出电流可以是Im或是对应V的实际阵列电流Iout,便于系统的动态调试、观测。模型子系统中T、S为实际环境温度、太阳辐射强度,U+、U-为光伏阵列输出电压,Vm、Im为光伏阵列最大功率点电压、电流,内部参数Voc、Isco、Rsh、Rs等可以根据厂家提供的技术数据修改。
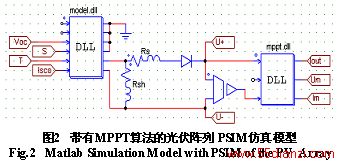
上述模型是根据电子学理论构建的,能够模拟外界环境温度、光照强度变化对PV电池特性的影响,参数可以模拟实际光伏电池,同时兼顾MPPT仿真算法,所以该模型具有较高的灵活性和仿真精度。
将带有通用MPPT算法的光伏阵列仿真模块封装后,用于图3所示的单相光伏并网系统的动态仿真。系统输入电源采用上述光伏阵列模块;利用PSIM模型库提供的元器件构成逆变单元;其中PDF.dll控件是采用C编写的具有参数自寻优的伪微分结构(PDF——Pseudo-derivative Feedback)的调节器,根据目标函数优化调节器参数,提高响应迅速,有效改善系统稳定性、抗扰性[8]。