摘要：提出一种考虑发电机有功出力调度的输电能力计算方法，该算法结合了连续性潮流计算方法和一些优化算法的优点，可由一个可行的潮流解出发，计算出各发电机有功出力随系统负荷增加时的变化情况以及考虑发电机调度时的系统输电能力。经过验证，该算法能有效地提高系统的输电能力，这对于在系统接近输电能力极限时如何通过调度发电机的出力，使系统维持一定的稳定裕度从而保持正常运行具有重要的意义。
关键词：系统输电能力 连续性潮流计算 最速下降法
1 引言
随着现代电力系统的发展，能源供应中心与负荷中心相分离已经成为一种必然的趋势。电力市场化作为电能高效、可靠管理的一种手段，越来越受到广大专家学者的重视 。在电力市场理论中，系统输电能力是一项重要的评估和交易指标，它是指在特定的系统运行情况下互联的电力系统通过区域间的所有联接线将电能可靠地由一个区域输送到另一区域的能力［1］。为了充分利用现有输配电系统，提高系统稳定裕度，计算系统输电能力的算法应该尽可能地模拟系统的运行情况以求得最大的系统输电能力。
目前求解系统输电能力的方法主要有两种：连续性潮流计算法（简称CPFlow法）和最优潮流法（简称OPF法）。CPFlow法是计算输电能力的一种有效方法［2］，它通过在常规潮流方程中添加连续性参数，克服了常规潮流计算方法(如牛顿法、快速解耦法等)在系统运行点接近鞍结分岔点时发散的问题。OPF法是将系统输电能力的求解问题转化为求解满足系统潮流方程（等式约束）和其它一些约束条件（不等式约束）的情况下系统的最大负载能力［3］问题，目前所采用的技术包括预测校正内点法等一些优化方法。在这两类方法中，发电机出力的增长方向都是通过预先设定的方式确定的，这与实际系统运行情况不相符合。在实际系统中，当负荷水平变化时，各发电机的出力模式可以通过调度进行调整，调整的方式是多种多样的。将发电机出力按固定的模式调整，所获得的计算结果趋于保守，从而限制了输电系统的利用率，造成现有资源的浪费。
考虑到电力系统计算本身的特点和发电机有功出力对系统的重要影响，本文将CPFlow法与最优化方法相结合，利用CPFlow完成给定发电机调度模式下的电力系统输电能力计算，而利用最优化方法不断确定系统负荷水平变化时的发电机最佳出力方式。通过二者的结合可以确定出以最大输电能力为目标的发电机调度模式。算例表明，与未考虑发电机调度模式变化时的计算结果相比，本文算法确定的反映系统输电能力的有关量得到很大的提高。利用这种算法确定系统的输电能力更能体现实际电力系统的情况。
2 基本数学模型
通过优化系统内发电机有功出力获得系统输电能力，可以被模拟为一个静态的非线性最优化问题。问题的目标是在满足电力系统中各种设备限制条件的情况下，通过优化系统发电机的有功出力求得系统输电能力的最大值。该问题的数学模型如下［4］：
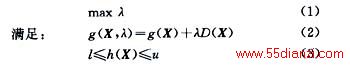
其中，标量λ＝f(X)表示在其他运行方式不变、各个发电机出力方式确定的前提下反映系统输电能力的量，又称母线注入条件数。矢量X＝(x1，x2，…，xn)表示系统内可以调节有功出力的发电机的有功出力值，该矢量中可以包括系统内所有的发电机,也可以根据需要设定可供调节的发电机。矢量方程组g(X，λ)是一组加入标量λ的参数化潮流方程。方程组g(X)表示标准的潮流方程组。D(X)∈Rn是系统负荷及发电机有功出力增长的方向，简称方向矢量。如果某一母线负荷不变且该母线上没有发电机参与调度，则D(X)中相应元素为0，母线注入条件数λ与增长方向D(X)的乘积是每次计算时各母线实际的有功变化量，有关式(2)的详细表达式参见文献［3］、［4］。不等式约束(3)反映各种设备参数的取值范围，这些限制可以包括各母线电压、有载调压变压器的抽头位置 、移相器的移相角、发电机的有功和无功出力以及支路的有功和无功潮流等参数的允许范围。
主要计算过程包括以下两部分：
(1)求解给定发电机调度模式下以λmax来反映的系统输电能力，计算相对于各发电机有功出力的灵敏度。与λmax相对应的点在状态空间中对应于方程(2)的鞍结分岔点。在求解此类问题时，所采用的计算工具是CPFlow。CPFlow是追踪系统运行点随负荷或发电机有功出力变化的一种有效工具，它具有计算速度快、可靠性高等优点，非常适合这一部分的应用要求。
(2)根据第一部分确定出的λmax相对于各发电机有功出力的灵敏度信息，确定使得λmax可以进一步增大的发电机调度模式，确定负荷增长时各发电机应承担的有功功率。计算各发电机有功出力变化量时运用的是经过改进的最速下降法。最速下降法［5］是梯度法与最优步长控制相结合的一种优化方法，其应用范围是求解无约束极值问题。在本算法的应用中，由于发电机输出最大功率的限制，根据最速下降法确定的发电机有功出力需作适当的调整，为此需对最速下降法进行改进。这种改进主要体现在对算法收敛条件的调整上。依据电力系统的实际运行情况，改进后的最速下降法的收敛条件如下：
经过计算，λmax相对于各发电机出力的灵敏度中最大值的绝对值小于预先给定的计算精度，则停止计算并认为当前解为最优解；
或者经过若干次计算后，各发电机均到达其有功出力的极限值，而且根据灵敏度计算，各发电机还应该继续向越限的方向调节出力，则此时计算停止，并根据之前的计算结果，确定一组最优的发电机状态。
3 算法实现
求解系统输电能力的最大值是在现行的运行状态下通过调节系统内发电机的有功出力来达到的，因此要求算法的起始点必须是可行的运行点。考虑发电机有功调度影响的系统最大输电能力计算的基本步骤如下：
第一步：给定系统当前运行状态，即相关的电力系统潮流计算数据，包括母线、发电机、负荷、变压器等数据；给定算法控制信息，包括最速下降法的收敛极限ε，负荷调整量的截止极限ρ等。此时系统的总负荷记为P（0）L，计算中系统总负荷的增量初值取为ΔPL＝200 MW。
第二步：在第k个负荷水平及发电机有功出力状态下调用CPFlow计算出相应的以
（k＝0，1，…）描述的系统输电能力。将计算结果与此时发电机的状态记录下来。
第三步：计算对各发电机有功出力的灵敏度，并对发电机有功出力进行重新调整。因为和各发电机有功出力之间的关系无法用解析式表示出来，在本算法中由对各发电机有功出力的灵敏度来代替梯度法中所要求的梯度方向。灵敏度的计算方法如下：
对于有功出力尚未达到上限或下限的发电机，将有功出力分别按其最大出力的2%进行调整；对于有功出力已经达到上限或下限的发电机，将有功出力沿离开限制值的方向按其最大出力的2%进行调整，各发电机有功出力的变化量记为
。
各发电机有功出力分别调整后，调用CPFlow分别计算各机调整后的系统输电能力,对第i台发电机，结果记为
。用减去得到区域间传送能力在调整第i台发电机出力后的变化量，记为d。经过计算得到反映区域间传送能力的相对于每台发电机有功出力的灵敏度：
其中 n为系统内的发电机台数。
如果满足收敛条件，则根据最速下降法的原理可知，当前解为最优解。此时输出计算结果，计算结束；否则继续下一步计算。
第五步：为了保证在负荷增长过程中，系统保持给定的备用率不变，需要对各发电机的灵敏度重新进行调整。首先求取系统中发电机灵敏度的平均值
，然后对每台发电机相应的灵敏度进行调整，调整后的灵敏度为：
第六步：判断各发电机是否能够按灵敏度计算所得的方向调整其有功出力。如果是 ，则继续下一步计算；如果各发电机的有功出力限制使得所有发电机有功出力都不能再进一步调节，则在已有的计算结果记录中选取最优解，输出计算结果，计算结束。
第七步：增加系统负荷，使得系统的总负荷为：
在新的负荷水平下计算系统的基态潮流。如果潮流方程不收敛，则先将系统恢复到上一步的状态，并将ΔPL减小为原值的四分之一，然后重新进行本步计算，直至潮流方程收敛。若ΔPL≤ρ时系统仍不收敛，则在已有的计算结果记录中选取最优解，输出计算结果，计算结束。
第八步：采用黄金分割法确定第k＋1个负荷水平及发电机有功出力调整量。设定黄金分割法的区间为［a，b］，其中a、b的起始值分别为0、200。计算当全系统负荷调整量为b时，系统的发电机的调整情况，具体做法如下：
按灵敏度信息
对各发电机有功出力进行分配，使得为正的发电机的有功功率调整量的总和为b，使为负的发电机的有功功率调整量的总和为－b（注：这样可以保证系统中发电机有功备用率不变，若系统内发电机有功备用率可以随负荷的增大而减小，则可使为负的发电机的有功功率调整量的总和小于为正的发电机的有功功率调整量的总和b）。
检验黄金分割法的区间长度是否小于截止极限δ。如果是，则转入算法第二步；否则继续下面的算法。
调用CPFlow计算当调整量为分割区间的两个黄金分割点x1、x2时系统的区域传送能力f(x1)和f(x2)。其中：
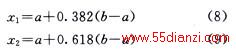
比较f(x1)和f(x2)的值，并根据黄金分割法的规则重新定义黄金分割法的区间 ，具体的定义方法请参阅文献［5］。
循环执行本步算法直至黄金分割法的区间长度小于截止极限δ。
4 算例结果与分析
本文采用的算例为天津电网未来某年份220kV及以上输电网。该系统包括66条母线 、15台发电机、3台500 kV／220 kV变压器、1台调相机和2台无功补偿设备。系统总负荷为4500 MW，天津本地发电机的出力为3700 MW。在计算中将北京电网安定500 kV母线设为系统的平衡母线，系统有功功率的不足均由平衡母线来补足。因此，当系统到达电压稳定极限点时安定500 kV母线的有功出力就等于京津电网间的系统输电能力。
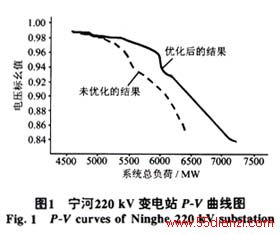
如果计算系统输电能力时不考虑发电机有功功率调度方式的变化，此时系统的P－V曲线如图1中的虚线所示，系统到达电压稳定极限点时的总负荷为6378．72MW，京津电网间的系统输电能力为
λ＝6378．72－3700＝2678．72 MW
以本文所提出的算法进行计算时，系统到达电压稳定极限点时的总负荷为7123．74MW，京津电网间的系统输电能力为
λmax＝7123．74－3700＝3423．74 MW
与直接计算的结果相比，系统输电能力由2678．72 MW增至3423．74 MW，增加了745．02MW，将近28%，可见本文所提出的算法有很好的效果。图1给出了两种情况下220 kV宁河变电站的P－V曲线。
5 结束语
本文针对目前求解系统输电能力的方法中常常缺乏对发电机有功出力优化调度的合理考虑，提出了一种将CPFlow与优化方法相结合以确定系统内负荷水平变化时发电机有功出力的调度方法。实际系统计算表明，所发展的算法能有效地提高系统的输电能力，是系统输电能力常规计算方法的一种有效的改进。
