The design of HVDCnonlinear main controler
DU Hongji，DINGyi
(Nanjing University ofScience＆Technology，Nanjing 210094，China)
Abstract：By applying the relation extent method，an HVDCnonlinear main controlleris designed．The main controllerincludesstabilization－controller and unstabilization －controller，they worksin differentconditions．Stabilization－controller makes rectifier workingin definite DCcurrent mode，and makesinverter workingin definite extinction angle mode．unstabilization－controller makesrectifier’sfiring－angleinvari－able，and makesinverter worksin definite DCcurrent mode．The main controller’s effectivenessis demonstrated withthe simulation results．
Key words：HVDC；nonlinear；controller
1 引言
高压直流输电(HVDC)系统的稳态运行方式是整流器运行于恒定电流状态以保持系统的稳定，而逆变器运行于恒定熄弧角状态以维持足够的换相裕度［1］。但稳态条件不可能在任何情况下都得到满足，在系统降压运行等非稳态运行条件下，系统切换为逆变器运行于定电流方式而整流器运行于定触发延迟角方式。稳态和非稳态运行方式的配合可以更好的保持系统稳定。稳态控制器和非稳态控制器并列构成主控制器，如图1所示。常规的控制器设计方法是首先对系统模型近似线性化，然后设计PI控制器或PID控制器。当系统受到的扰动较大，偏离工作点较远时，按这种方法设计的控制器将难以产生有效的控制作用，本文尝试采用关系度方法设计了HVDC非线性主控制器。
2 关系度方法
对于某一系统输出y(t)，若控制量u可以直接控制它的某一阶导数
(k为非负整数)，即：
式中M为可测向量。
函数f满足：若u能取遍(－∞，＋∞)，则f也能取遍(－∞，＋∞)，则u能间接控制y(i)(t)(i＝ 0，1，2，…，k－1)，且称输出y(t)与控制量u的关系度为k，记为R(y，u)＝k。如果记
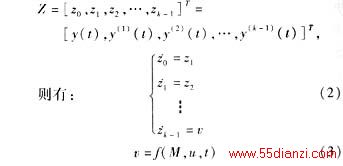
对于式(2)，可将其作为近似线性系统(伪线性系统)，应用线性系统理论加以分析，得到使得渐近稳定的虚拟控制量，然后由式(3)可解出真实控制量。用李导数法可以求出两个量的关系度［2］。若R(y，u)＝0，即y(t)＝f(M，u，t)，那么令f(M，u，t)＝0，可得出使y(t)在任意时刻精确的等于0的控制规律u。若R(y，u)＞0，则不可能得出使y(t)在任意时刻均精确等于0的控制规律，因为R(y，u)＞0表示有延迟环节存在，此时只能找到使y(t)渐近趋于0的控制规律。与微分几何、逆系统等方法相比，这种关系度方法物理意义明确，而且推导简单明晰。为了保证设计的严密，本文采用零动态方法进行了稳定性验证。
3 稳态控制器的设计与稳定性验证
高压直流输电系统在正常运行条件下，通过控制换流器阀桥的触发角，使整流器工作在定直流电流方式。这样可以保证输电系统的传输功率，并增强交直流系统的稳定性；逆变器工作在恒定超前角方式，以保证高压直流系统从电网中吸收的无功功率最少。
3．1 稳态控制器的设计
由参考文献3，直流输电线路的动态方程为：
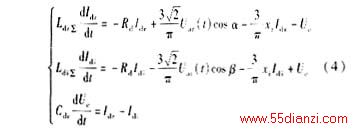
其中
分别表示整流侧和逆变侧平波电抗器的电感；Ld，Rd分别表示二分之一直流线路的电感和电阻；Idr和Idi分别表示整流侧和逆变侧的直流电流；Var(t)，Vai(t)分别表示整流器和逆变器的交流侧线电压；α为整流器的触发延迟角；β为逆变器的触发超前角； xr，xi分别为整流器、逆变器换流电抗；Cdc为直流输电线路对地的总电容；Vc为电容上的电压。
对于整流器，为了在任何时刻都能保持定直流电流运行，令 
联立式(4)和式(5)即可得到高压直流输电控制系统的稳态数学模型。
将α视为控制量，即uα(t)＝α，无须计算李导数就可以看出y1和uα(t)的关系度为1。
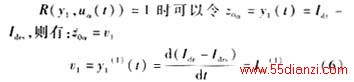
由(4)式和(6)式可得：
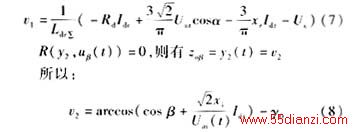
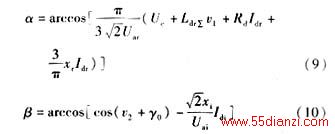
在上述控制规律作用下，原非线性系统成为伪线性系统，其中：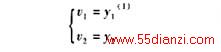
3．2 稳态控制器的稳定性分析
由理想控制目标y1(t)=y2(t)=0,可得零动态方程：
这个零动态方程是线性的。当且仅当Reλi(A)<0(i=1,2)时，零动态渐近稳定在全局唯一平衡点η0＝－A－1 b处。由于
根据Routh判据，零动态稳定的充要条件为Rd>
且在此条件下整个稳态非线性控制器渐近稳定。
4 非稳态控制器的设计与稳定性验证
4．1 非稳态控制器的设计
此时整流器触发延迟角保持恒定，即α＝αmin而逆变器必须保持直流电流恒定，所以设：
综合式(4)可得非稳态下HVDC系统控制的数学模型：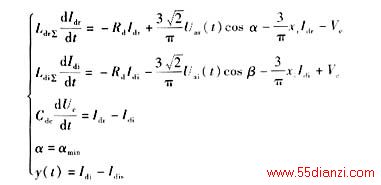
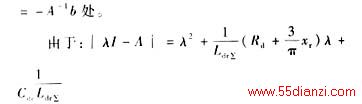
在上述反馈控制规律作用下，系统成为伪线性系统，且：y(1)＝v
4．2 非稳态控制器的稳定性分析
由于系统包含有二阶零动态，整个系统的稳定性取决于零动态的稳定性。 
当y≡0时，可得系统的零动态方程：
此零动态方程是线性的。当且仅当Reλi(A)＜ 0(i＝1，2)时，零动态渐近稳定在全局唯一平衡点η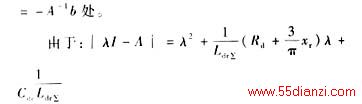
根据Routh判据，零动态渐近稳定，且整个非稳态控制器渐近稳定。
5 仿真验证
本文采用电力系统分析软件包EMTDC/PSCAD3．0对稳态控制器和非稳态控制器进行了仿真。根据CIGRE的标准高压直流输电系统数据，仿真时取6脉波桥数为2，直流输电线路额定电压为500 kV，直流线路额定电流为2 kA，直流输电线路长度为1367．65 km，线路电阻为19．108Ω，直流线路电感(包括平波电抗器)为0．5968 H，逆变器换流电抗为9．522Ω，整流器换流电抗为21．4245Ω。
首先对稳态控制器进行仿真。在稳态运行条件下，定逆变器的熄弧超前角γ为15°，并对整流器触发延迟角α进行限幅，取5°≤α≤90°。在给系统 20％的初始扰动后，仿真结果如图2所示。
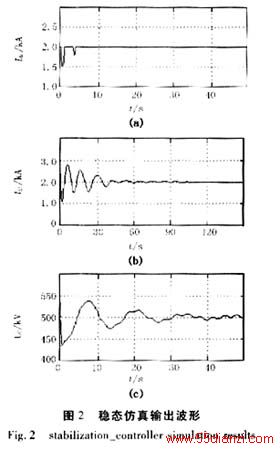
仿真输出波形中可以看出，整流器电流很快就达到稳定，这是因为稳态控制器对整流器的定电流控制作用可以很好的保持整流侧电流的恒定。逆变器电流和直流电压衰减也较快的达到了稳定。可见在本文所设计的稳态控制器作用下，系统是稳定的。
对非稳态控制器仿真仍取与稳态控制器仿真同样的系统参数。综合考虑提高传输效率和确保触发前阀上有足够的电压，取α＝αmin＝5°。给系统施加20％的初始扰动后，仿真输出波形如图3所示。
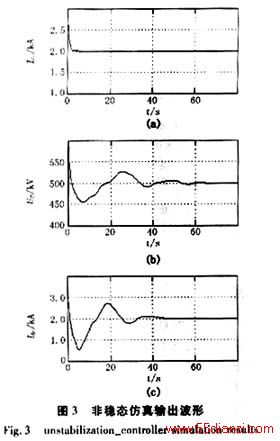
从仿真结果可以看出，逆变侧电流在非稳态控制器作用下很好的保持了恒定，直流电压和整流侧电流也很快趋于稳定，可见在本文所设计的非稳态控制器作用下，系统是稳定的。
参考文献
［1］李兴源．高压直流输电系统的运行和控制［M］．北京：科学出版社，1998
［2］高为炳．非线性控制系统导论．北京：科学出版社［M］．1988
［3］卢强，孙元章．电力系统非线性控制．北京：科学出版社［M］．1993
本文关键字：控制器 电工文摘，电工技术 - 电工文摘
