索南加乐1, 宋国兵1, 许庆强1, 张健康1, 赵志华2

（1.西安交通大学电气工程学院, 陕西 西安710049
2. 许昌继电器研究所, 河南 许昌 461000）

    摘  要：文中给出了一种新的相量滤波器的设计方法，该滤波器的实部和虚部函数具有一致的幅频特性和对基波信号的相位正交性，且滤波器数据窗长度的选择任意，有效地解决了短窗滤波器的设计问题，采用该方法设计的滤波器已用于高压微机继电保护装置，取得良好的运行效果。
    关键词：电力系统；继电保护；幅频特性；正交性；相量滤波器

1  引言
    基于相量法的电气量计算，因其数学表达式简单、直观且有利于计算机实现等优点，目前已被广泛用于电力系统的电气量测量、控制和保护[1~5]。相量算法主要是通过相量的实部和虚部计算幅值和相角，因此相量计算要求相量的实部和虚部相位（基频时）正交，对各次谐波幅频特性一致。这对获取相量实部和虚部的滤波器也提出了同样的要求：相位的正交性、幅频特性的一致性。全周波傅氏算法是一种广为采用的相量滤波器，它的余弦和正弦函数分别构成相量实部和虚部的FIR滤波器，实部和虚部滤波器的幅频特性对整次谐波是一样的，而对非整次谐波相差较大，其中，正弦滤波器消除非整次谐波的效果优于余弦滤波器。另外，全周波傅氏算法滤波器用于反应工频量的继电保护时，当故障发生后必须等待工频一周波的数据才能开始有效计算。对于超高速继电保护来说，这种滤波器响应时间过长，因而有必要进一步研究短数据窗的相量滤波器以提高继电保护的动作速度。目前，为了提高动作速度，常采用半周傅氏滤波器以及利用连续几点采样值来拟合相量的实部和虚部的滤波器[6]，以这两种方法实现的相量滤波器在基频时，其实部和虚部的相频特性是正交的，但对各次谐波和非整次谐波幅频特性差异非常大。最小二乘算法构成的相量滤波器数据窗虽可根据滤波器的性能要求或长或短，但和全周波傅氏相量滤波器一样，也存在实部和虚部的幅频特性对非整次谐波差别较大的问题。
    在继电保护中，为了及时、有效地获取故障分量，在故障发生后的不同时刻，需要由不同数据窗长度的滤波器来提取故障分量，且希望滤波器实部和虚部的幅频特性一致、在基频时相位正交。为满足继电保护的这种特殊要求，本文提出了一种相量滤波器的设计方法，它既兼顾了任意选择数据窗长度，又具有幅频特性一致和相频特性在基频时正交的特点。用该方法设计的一系列不同性能的滤波器已用于高压微机继电保护装置，并取得了较好的运行效果。
2　短数据窗正交滤波器的设计
2.1　基于两点采样值的相量滤波器的设计
    相量运算要求其实部和虚部的幅频特性一致，为此本节先由两点采样值导出具有幅频特性一致的相量滤波器的设计方法，然后由此推广到多点，从而得到一般相量正交滤波器的设计方法。
    设ik,ik+1是连续两点的采样值，对于基频来说，ik,ik+1的函数可以表示为

式中  Ｉ为基频分量的幅值；q为初相角；d为采样间隔，设一周波内的采样点为n，则d＝2p/n。 
    电流相量的实部和虚部瞬时值可表示为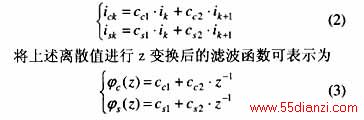

为了对式(3)的频率特性进行分析，现将其转换到复频域。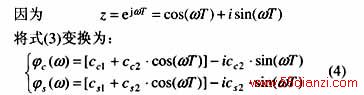

则  幅频特性可以表示为

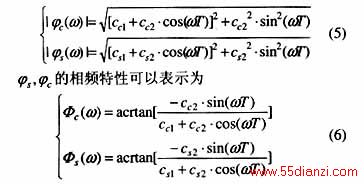
    由于正交滤波器要求φc,φs 的幅频特性一致，即│φc(w)│,│φs(w)│，由此得出以下联立方程组：

    另外，正交滤波器要求在基频时，φs(w)和φc(w) 的相位差应为p/2，即φs(w)超前φc(w) 的为p/2。由于在基频时有w=a0，所以有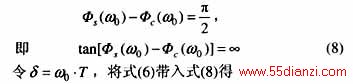

令δ=a0.T，将式(6)带入式(8)得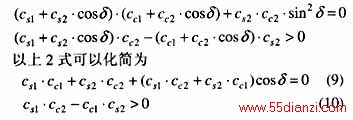

也就是说，只有方程组式(7)的解同时满足式(9)、(10)时，才有基频时φs(w)和φc(w)的相位正交。
    很明显方程组式(7)的解①、解②不满足式(10)，故可将其舍去。将解③、解④代入式(9)得

因为式(11)中的cosδ>0，必有cc1.cc2<0，即cc1、cc2异号。所以正交滤波器必须满足以下条件：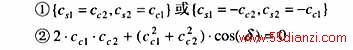

    由条件①和②可以求出正交滤波器的系数为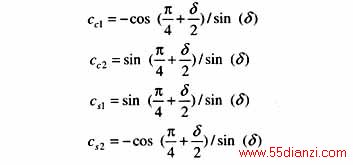

然后即可写出满足正交条件的2采样点正交滤波器函数φc和φs为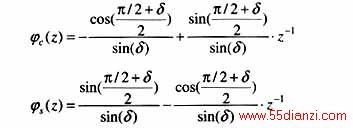

2.2　短数据窗正交滤波器的设计
    以上给出由ik和ik+1两采样点求出一对正交相量isk和ick的方法。若给定m+1个采样点ik ， ik+1,…,ik+m，通过相邻点的两两正交化，得到m 对正交相量。为这些正交化相量选择一个数据窗长度为m的窗函数，则得到m+1点数据长度的正交滤波器。该正交滤波器的实部和虚部函数表达式为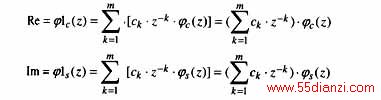

     这样，就可以得到一个数据窗长度为m+1的数字滤波器，m值不同，所得滤波器的数据窗长度也不同，从而可实现任意长度数据窗的正交相量滤波器的设计。由于φc 和φs是幅频特性一致的正交函数，实部、虚部所用数据窗函数相同，所以j1c和j1s也具有幅频特性一致性和相位正交性。由此, 可得到用m+1个采样点设计正交滤波器的一般方法：首先对m+1个点进行两点正交化，得到m对正交相量，然后根据性能需要，选择一个幅频特性满足设计要求的窗函数w(k)，再将窗函数和正交滤波函数级联，即可得所需滤波器函数。
    这里需要着重强调的是窗函数的选取问题。在正交滤波器的设计中，窗函数的选取尤为重要，它决定着滤波器的性能。现就常见的余弦窗和正弦窗为例，简要地说明窗函数与滤波器性能的关系：余弦窗为偶对称，对直流分量的抑制能力较差，对高次谐波有较好的抑制能力；正弦窗为奇对称，对直流分量有较好的抑制能力，对高次谐波抑制能力较差。
3　性能分析
3.1  仿真条件
    本文给出了每周12点采样条件下的全周傅氏相量滤波器、半周傅氏相量滤波器、三点拟合相量滤波器的幅频特性，并与本文所述相同数据窗长度的幅频特性一致的正交相量滤波器的幅频特性进行比较。本文在仿真中，全周和半周正交相量滤波器的窗函数为余弦窗。
    为了较为直观地进行幅频特性的定性分析和定量比较，每种情况下都给出了幅频特性图，并将每个图中的特征点数据(包括各区段的最大最小值和特征频率点的值)列于相应的表中。由于正交滤波器的实部、虚部具有相同的幅频特性，故正交滤波器幅频特性表中只给出其实部幅频特性参数。
    以下仿真是在每周采样12点，即K＝12，δ=π/6的条件下给出的，此时的正交滤波器函数表达式为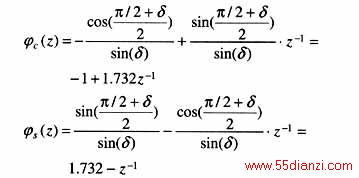

3.2　全周相量滤波器
    全周傅氏相量滤波器的传递函数为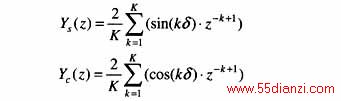

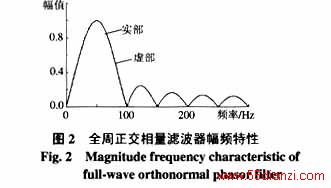
    全周傅氏相量滤波器的幅频特性如图1所示。全周正交相量滤波器的传递函数为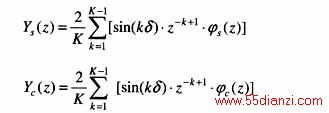

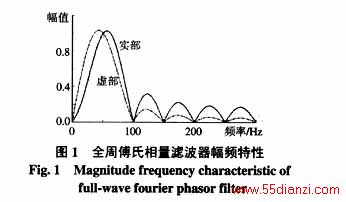
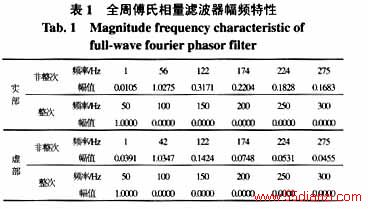
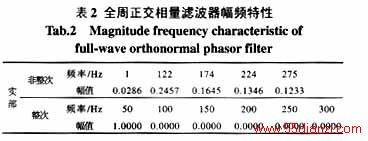
    全周正交相量滤波器的幅频特性如图2所示，表1给出了。从图1、2可以看出：全周傅氏相量滤波器实部和虚部的幅频特性不一致，它们对整次谐波的响应相同，非整次谐波差异较大；其中实部幅频特性的边瓣较大，虚部幅频特性的边瓣较小；而全周正交相量滤波器实部和虚部的幅频特性完全相同，边瓣大小也介于全周傅氏相量滤波器实部和虚部幅频特性之间。从表1数据可以看出，全周傅氏相量滤波器实部幅频特性对56Hz的信号放大作用最强，达到1.0275，虚部幅频特性对42Hz的信号放大作用最强，达到1.0347。从表2中给出的特征点数据可以看出，正交滤波器对50Hz信号的放大倍数为1，此频率下的放大倍数为最高。经表1、2数据对比可知：在基频的整数倍频率时，除50Hz对应的放大倍数为1外，其余整数倍频率处的放大倍数全为0；滤波器对非整次谐波的放大倍数在122、174、224、275Hz处达到极大值点，对应的放大倍数分别是：全周实部0.3171、0.2204、0.1828、0.1683；全周虚部0.1424、0.0748、0.0531、0.0455；正交滤波器实部0.2457、0.1645、0.1346、0.1233。虚部与之相同。由以上数据对比可以明显地看出：全周正交相量滤波器对非整次谐波的响应介于全周傅氏相量滤波器的实部和虚部之间，对整次谐波和基波的响应与全周傅氏相量滤波器相同。

3.3　半周相量滤波器
    半周傅氏相量滤波器的传递函数为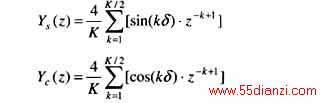

半周傅氏相量滤波器的幅频特性如图3和表3所示。半周正交相量滤波器的传递函数为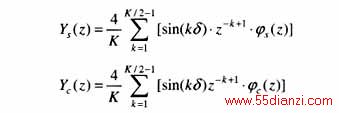

半周正交相量滤波器的幅频特性如图4和表4所示。

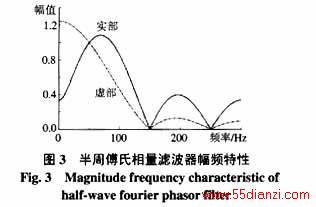
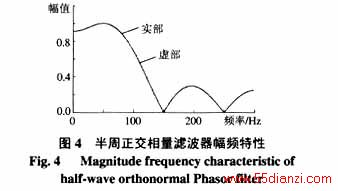
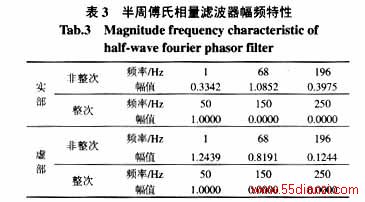
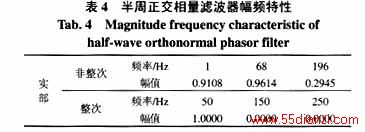
    从图3可以看出，半周傅氏相量滤波器实部和虚部的幅频特性明显不一致，其中，实部受非整次谐波影响较大，虚部受非整次谐波影响较小。而半周傅氏相量滤波器实部和虚部受非周期分量的影响也不一致，其中，虚部受非周期分量的影响较大，实部受非周期分量的影响较小。从图4可以看出，半周正交相量滤波器实部和虚部的幅频特性相同。从表3、4中的数据还可以看出，半周正交相量滤波器对非周期分量、非整次谐波的放大倍数也介于半周傅氏相量滤波器的实部和虚部之间。
3.4　3点相量滤波器
    3点拟合相量滤波器[1]的传递函数为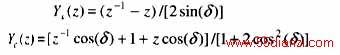

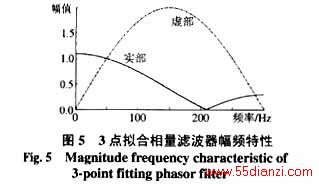
3点拟合相量滤波器的幅频特性如图5和表5所示。

2点加法正交相量滤波器的传递函数为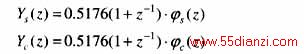

2点加法正交相量滤波器的幅频特性如图6和表6所示。

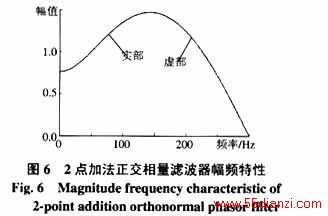
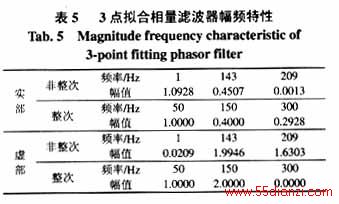
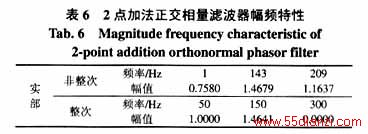
    从图5、6可以看出，与全周半周相比，3点拟合相量滤波器实部和虚部的幅频特性差异更大，除了在基波时的幅频特性相同外，其余频率处差异较大，其中虚部对3次谐波放大尤其明显。而2点加法正交相量滤波器实部和虚部的幅频特性相同，从表5、6中的数据也可以看出，2点加法正交相量滤波器对非整次谐波的放大倍数也介于3点拟合相量滤波器的实部和虚部之间。
4  结论
    由图1~6的幅频特性和表1~6的幅频特性特征点数据可以得出如下结论：
    （1）随着数据窗的减小，传统滤波器实部和虚部的幅频特性差异逐渐增大。而正交相量滤波器幅频特性是一致的，且该特性与数据窗长度无关。
    （2）在相同的采样频率和采样点数情况下，正交相量滤波器对非周期分量和非整次谐波的抑制能力都介于传统方法的实部、虚部幅频特性之间。
    （3）正交相量滤波器的窗函数长度和类型可以任意选择。也就是说，可通过对滤波器的快速性要求来选择数据窗长度，通过对滤波器特性的要求来选择数据窗类型。这一特性使得针对滤波器快速性和性能的设计变得简单，该优越性是传统相量滤波器所无法比拟的。
    该算法已被用于许继集团有限公司的WXH-800系列数字式微机高压线路保护装置，多年来的运行结果表明，该算法与传统滤波算法相比效果有不同程度的改善，尤其在短数据窗时候，性能改善得更为明显。

参考文献

[1]  Liancheng Wang. Frequency responses of phasor-based microprocessor relaying algorithms [J]. IEEE Trans. on Power Delivery, 1999,14(1)： 98-105.
[2]  José A. de La O. New family of digital filters for phasor computation [J]. IEEE Trans. on Power Delivery, 2000,15(1)：86-91.
[3] 张伏生,耿中行,葛耀中(Zhang Fusheng, Geng Zhongxing, Ge Yaozhong).电力系统谐波分析的高精度FFT算法(FFT algorithm with high accuracy for harmonic analysis in power system)[J].中国电机工程学报(Proceedings of the CSEE).1999,19(3)：63-66.
[4] 赵文春, 马伟明, 胡安(Zhao Wenchun, Ma Weiming, Hu An).电机测试中谐波分析的高精度FFT算法(FFT algorithm with high accuracy for harmonic analysis in the electric machine)[J].中国电机工程学报(Proceedings of the CSEE).2001,21(12)：83-87.
[5] 胡志坚,张承学,陈允平,等(Hu Zhijian, Zhang Chengxue, Chen Yunping, et al). 滤除衰减非周期分量的微机保护算法研究(Study on protective algorithm for elimination of decaying aperiodic component) [J].电网技术(Power system technology).2001,25(3)：7-11.
[6] 孙军、陶惠良译(Translated by Sun Jun, Tao Huiliang)，微处理机式继电器和保护系统(Microprocessor relay and protection system)[M]，重庆：重庆大学出版社(Chongqing：Chongqing University Press)，1990.

本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘