贾宏杰，余贻鑫，王成山
（天津大学电气自动化与能源工程学院，天津300072）
摘要：利用非线性动力系统的基本理论，并借助于一个简单的电力系统，给出了电力系统中导致混沌出现的两种不同的途径。运用Piocaré截面和Piocaré映射技术，深入研究这两种途径的表现形式、内在规律、引发机理，并进一步讨论了它们与电力系统扰动间的关系。由于混沌现象存在时，系统运行参数将伴随持续无规则的振荡，这在电力系统运行中是绝对不允许的，而弄清楚混沌的产生机理，将有利于对它的预防。
关键词：电力系统；混沌；稳定性；扰动
1 引言
近年来，随着对电力系统稳定性的深入研究，国内外学者相继发现在电力系统中存在十分复杂的混沌现象［1～5］。混沌是非线性系统中各参数相互作用导致的一种非常复杂的现象。它在电力系统中出现时，将伴随系统运行参数持续无规则的振荡，严重危害系统的运行安全，而要在电力系统中有效地预防和消除它，首先应弄清楚其引发机理和产生途径。本文的工作将借助非线性动力系统的一些基本理论和工具，研究电力系统中诱发混沌现象的两种途径：①从一个不稳定的平衡点出发，在未受任何扰动情况下，系统最终收敛到混沌吸引子；②系统经较大的扰动，本身具有很大的动能，其扰动后的终态呈现为混沌。并揭示相应的演变过程和内在规律。
2 电力系统中的混沌现象及其产生途径
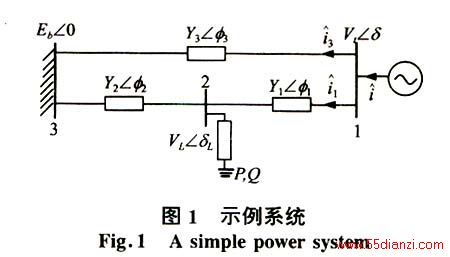
混沌现象是“在完全确定性的模型下产生的不确定性现象［6］”。从对混沌现象的定性描述中，不难看出，很难为混沌本身下一个完整准确的定义。在长期的研究中，人们只是感性地认识到混沌系统Ψ所存在的一些典型的性质［6］：Ψ是有界的（因而也称之为奇异吸引子）；Ψ的任何轨道都是不稳定的；Ψ含有不可数无穷多个在Ψ中稠密的轨道；Ψ的周期轨道是稠密的；轨道对初值有敏感的依赖性，即任意2个轨道不论其初始点如何靠近都将随t的增加而截然不同，等等。下边笔者将利用如下图1所示的一个简单的3节点系统，研究和讨论电力系统中混沌出现的两种途径。
2.1 系统模型
图1所示系统中节点1是发电机节点，节点3是无穷大母线，节点2为含有动态负荷特性的负荷节点，系统模型如下：
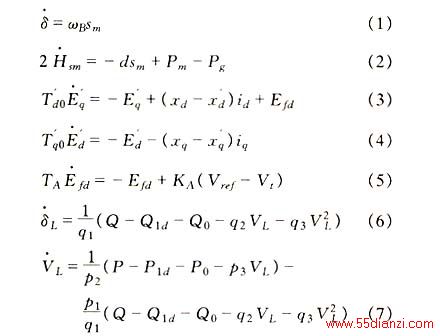
上述式中各参数的含义参见文［2］和文［5］。
系统模型的一般形式可表示为
当发电机具有快速励磁时，式（8）的状态变量为
；而当发电机为经典模型时，状态变量变为x＝［δ，sm，，δL，VL］T，此时若Y3取值为0，则该模型与文［2］中的所用模型相同，但由于文［2］H取值不在实际物理参数范围内，本文对其进行了修正。本文研究中，分岔变量λ仍取为Q1 d。
2．2 连续倍周期分岔导致的混沌
图1所示系统中，当发电机具有快速励磁装置，初始点取为：x0＝［0．761 115 5，0，1．332 678，－0．328 327 0，4．198 358，0．239 607 5，0．779 529 6］T，TA＝0．05，KA＝140，Q1 d取如下2个初值（其中Case 1条件对应着系统的一个平衡点，而Case 2在数值上仅与Case 1相差10－7）：
Case 1 Q1 d＝1．203 000 0（图2中用实线表示）；
Case 2 Q1 d＝1．203 000 1（图2中用虚线表示）。
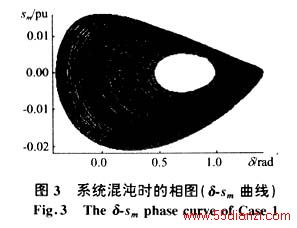
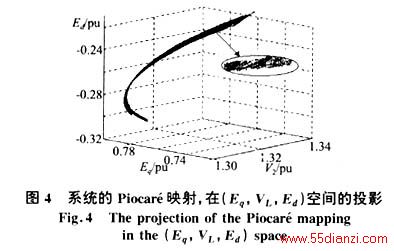
对系统进行仿真，可得到图2－4所示的结果。其中图2给出了两种情况下发电机角度δ随时间变化的曲线；图3给出了Case 1的δ－sm图；图4则绘出了Case1在如下Piocaré映射［6］上（在（Eq，VL，Ed）三维空间中）的投影：
式中 δc为角度的振荡中心：
从图2－4中，可以看出以下几点：
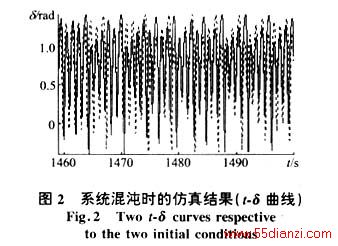
（1）如上所述，混沌系统的轨迹对初始点具有敏感的依赖性，此特征在图2中十分明显，例如当Q1 d取值仅相差10－7，而其相图在经历一段时间演变后，将完全不同；
（2）混沌现象是与持续、有界而又不规则的系统振荡相联系的，其振荡过程是相当稳定的（选用不同的积分方法，积分达20 000 s均可得到相同的结果，作为研究，此时间可认为足够长）；各种周期轨道，在混沌系统中稠密（图3）；同时任何一种周期轨道在混沌区域内都是不稳定的，即在混沌区域内无法找到完全相同的片段；
（3）Piocaré映射分布在有限空间范围内（说明该系统是有界的），其形状如一个扭曲带子，且一端有分叉结构（图4）。同时，此带状体的每一个局部空间内点的分布并不均匀，形成斑状结构（见图4中的放大部分），说明系统的Piocaré映射具有精细的结构[6]，当仿真的点数增加时，精细结构将更加明显。
在关于混沌的研究中，一种常见的途径是系统通过连续的倍周期分岔导致混沌出现，即系统由最初的单周期分岔出倍周期、接着出现4倍周期、8倍周期、……，若此过程持续下去，系统最终将出现混沌现象。在图1系统中，我们捕捉到这一种诱发混沌出现的途径：发电机采用双轴模型带快速励磁，参数取值同上，仍采用式（9）的Piocaré截面Θ，并将系统与Θ交点x处的δ坐标定义为 δ，用它做为分岔图的纵坐标，即
相应的系统分岔图示于图5。
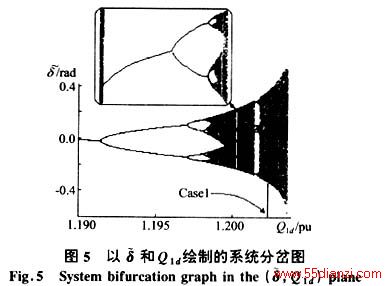
当Q1 d＜1.191 5时系统中存在着稳定的周期解，当Q1 d在1．191 5～1．197 0之间时存在着稳定的2周期轨道，接下来系统出现4周期（Q1 d≈1．197 0）和8周期（Q1 d≈1．198 08）……直至系统中出现混沌（Q1 d≈1．198 45），系统中存在有稳定的奇异吸引子。由典型的混沌系统，如Logistic、Loronz和Rossler的分岔图可知，混沌区域内应有稳定周期轨道组成的窗口存在［6］，将任一窗口放大后，将得到与原分岔图相似的结构，即混沌系统的分岔图具有分形结构，本系统也不例外。当Q1 d≈1．201 36时，系统出现了稳定的3周期轨道，此后，系统还相继出现了6周期（Q1 d≈1．201 525）和12周期（Q1 d≈1．201 559）……直至系统再次出现稳定的奇异吸引子（Q1 d≈1．201 60），重归于混沌。在此过程中系统振荡的幅度变得越来越大，直至Q1 d≈1．203 5附近时，系统达到奇异吸引子稳定的临界状态，稳定的吸引子随之消失。
2．3 经由初始能量直接激发混沌
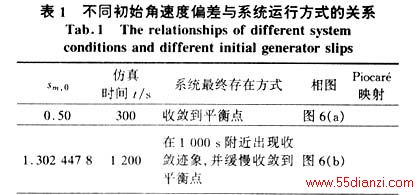
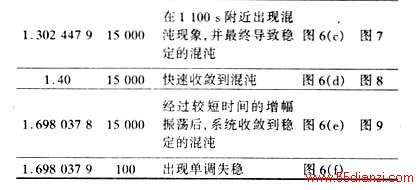
这里采用文［2］的模型，如前所述它对应于图系统的状态变量取为x＝［δ，sm，δL，VL］T，且Y3取值为0，并已对发电机的惯性常数做适当修正。将下边各种仿真计算的初始参数取为Q1 d＝10．894，δ0＝0．3 rad，δL，0＝0．2 rad，VL，0＝0．97。使发电机的角速度偏差sm，0在0～1．7之间缓慢变动，对系统进行数值仿真计算，所得结果示于表1、图6－9。
本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘
