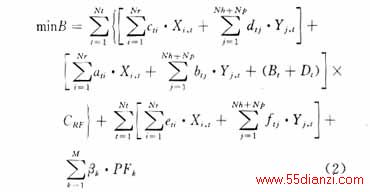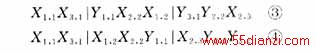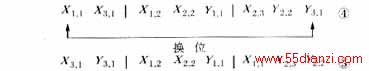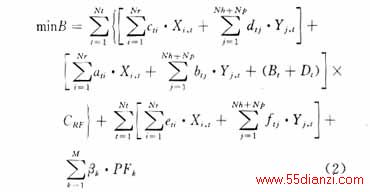
式中:Nt为规划期;minB为目标函数值;Nr为火电机组编号数;Nh为水电机组编号数;)为抽水蓄能机组编号数;Np为火电机组i第t年投产时的投资费用;bij为水电机组(包括抽水蓄能机组)j在第t年投产时的投资费用;CRF为资金收回系数;cti为火电机组i在规划期内的固定年运行费;dtj为水电机组(包括抽水蓄能机组)j在规划期内的固定年运行费用;eti为火电机组i在规划期内的可变年运行费用;ftj为水电机组(包括抽水蓄能机组)j在规划期内的可变年运行费用;Xi,t,Yj,t表示的都是一个0-1变量,1代表在第t年内投运了第i,j号机组,0则代表没有投运;Bt为在规划期t年新建电源除发电外的其他效益,如水电厂除发电外还可能具有的防洪、灌溉和航运等效益;Dt为在第t年首次投建水电项目所建大坝的费用;Bk为罚系数;PFk为染色体不满足约束条件k的计算值。
目标函数值min包括三部分:第一部分为电力系统投产支出和固定年运行的费用,由投入的机组型号、时间和各经济参数决定;第二部分为各段内投运机组在经过优化组合后,确定各机组的运行时间、状态,从而求出的可变年运行费用之和;第三部分为对应系统有关约束条件不满足的罚函数。
系统有关模型的约束条件主要包括系统电量平衡,发电机组最大最小出力约束,火电燃料消耗约束,水电水量消耗限制等约束。
(1)电量平衡约束
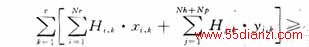
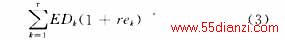
式中:xi,k在第¥规划段投运的编号为i的1类机组的容量;yj,k-在第k规划段投运的编号为j的2类机组的容量;Hi,k-在第k规划段投运的编号为i的1类机组的期望利用小时数;Hj,k-在第k规划段投运的编号为j的2类机组的期望利用小时数,若是抽水蓄能机组,Hj,k<0,这是因为抽水电量大于发电电量;EDk-k规划年的系统电量;rek-k规划年的电量备用系数。
(2)发电最大最小出力约束
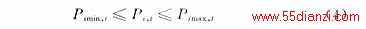
式中:Pi,t-机组"在-规划段内的出力;Pimin,t-机组i在t内的最小出力;Pimax,t-机组i在t内的最大出力。
(3)火电燃料消耗约束
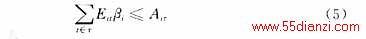
式中:Eit-火电机组i在时间段t内的发电量;Bi-发电机组i的平均燃料单耗;Air-机组i在总运行时间f内的燃料消耗限量。
(4)水电水量消耗限制约束

式中:Ejt-水电机组j在时间段-内的发电量;Bi-水电机组在时间f内的平均出力。
除上述主要约束条件外,还可以考虑调峰需求,最小开机容量,火电年利用小时数,抽水蓄能电厂等约束条件,在此不一一赘述。
3.3 模型原理框图及求解步骤
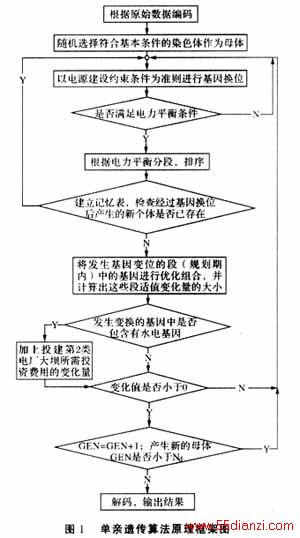
基于单亲遗传算法的电力系统电源规划模型原理框图,如图1所示。模型求解步骤如下:
(1)根据提供的待选机组的基本特征对各机组进行编码;
(2)随机产生满足最基本条件的染色体母体;
(3)以电源建设的约束条件为准则对染色体进行基因换位;
(4)新产生的染色体是否满足电力平衡条件,并按照最小冗余量原则,将基因按单位规划期(年)进行自然分段;
(5)构建记忆表,将已比较过的染色体写入其中,避免重复比较和计算;
(6)将发生基因换位位的段(规划期内)中的基因进行优化组合,使其目标函数值(这里又称作适值)最小,并计算出这些发生基因换位段的适值变化量ΔV;
(7)染色体发生基因换位中是否包含有水电基因(Y),如果没有包含水电基因,则求得变化量:ΔminB=ΔV;如果包含有水电基因,则存在水电大坝投建时间的确定问题,因此要将规划期内的水电基因统一考虑,确定大坝投建时间,计算出大坝投建费用、大坝社会效益的变化量Δ,并计及变换位基因的变化,同样求得变化量ΔminB=ΔV+ΔD;
(8)变化量ΔminB是否小于0,如果小于0,说明产生的新染色体比母体适应性更强,并将该染色体作为下一代的母体,GEN=GEN+1,进入下一代迭代。当迭代次数达到一定数值时,或者记忆表已经遍历所有组合,则停止迭代;
(9)解码,输出结果。
3.4 若干相关问题及处理
3.4.1 染色体的自然分段及排序
染色体自然分段即是以电力平衡为基本条件,按照最小冗余量原则以单位规划时间为间隔对染色体进行分段。染色体基因发生换位后,为避免重复操作,诸如
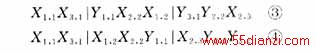
上述两个染色体实际上是等价的,因为各个机组的投建顺序是针对于不同的规划单位时间(年)来说的,在同一规划单位时间(年)内基因的排序是不影响其最后结果的,因此染色体都将按照④模式进行一次自然排序,避免重复计算与比较。其排序规则为:在同一单位规划时间内,基因排在基因前,在同类型的或基因间,将各基因按照编号(下标的第一个自然数)的顺序进行排序。
3.4.2 遗传操作
本文使用的PGA遗传方法只包含选择和基因换位两个操作。选择是将母体与经过一次迭代后生成的新个体比较后,选择适应性更强的染色体作为下一代的母体;基因换位操作是在分别属于不同规划单位时间(年)内的基因间进行的,例如将染色体④的第一段的X1,1基因与第三段的Y3,1基因发生换位,得到一个新的染色体⑤:
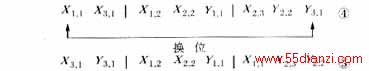
3.4.3 适值计算
本文使用的PGA的适值概念与TGA的完全相同,其计算方法也与TGA的几乎没什么区别。PGA的遗传算子对图式的破坏程度不如序号编码TGA的严重,子代个体保留了母体的绝大部分遗传特征,子代个体的适值表达式和相应的母体的适值表达式基本相同。因此,PGA在计算子代个体的适值时可以不重新计算整个适值表达式,而只需计算子代个体相对于母体的适值的变化量。这样,PGA的适值计算量可以大为减少。由于适值计算是提高遗传算法计算效率的瓶颈问题,PGA的这一优势可以使计算效率大为提高。
4 算例
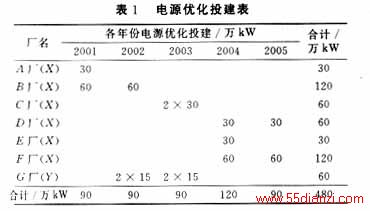
采用本文所述模型和常规动态规划模型对某电力系统14个待建电源进行五年规划的优化计算,计算中把规划期五年分为五个规划单位时间,每个规划单位时间为一年,充分考虑负荷情况,各规划电厂的机组容量、强迫停运率、备用系数、投资情况、运行费用、煤耗、大坝建设费用等条件,优化结果列于表1。
5 结论
本文所采用的基于自然分段式编码的PGA算法与遗传算法的基本原理相同,工作机制相似,采用遗传算法对上例进行验算,得到的结果一致。该方法与遗传算法比较起来,大大简化了遗传操作,利于应用计算机语言来实现,而且其适值计算量也大幅度减少。
综上所述,本文介绍的该方法比较起传统的遗传算法TGA,简化了遗传操作,提高了计算效率,并且不要求初始群体的多样性,也不存在"早熟收敛"问题。
该算法应该还有更广阔的发展空间和应用范围,如将单位时间可以定为季度或者月,将适用于今后对规划准确性与实时性的要求,不断提高其经济性与实用性。
参考文献
1 熊信银,吴耀武.遗传算法及其在电力系统中的应用.武汉:华中科技大学出版社,2002
2 侯煦光,等.电力系统最优规划.武汉:华中理工大学出版社,1991
3 陈皓勇,王锡凡.电源规划JASP的改进算法.电力系统自动化,2000,12(6):22-24
4 Jong B P,Young M P,Kwang R.An improved geneticalgorithm for generation expansion planning.IEEE Transactions on Power Systems,2000,15(3):916-922
上一页 [1] [2]
本文关键字:电源 电工文摘,电工技术 - 电工文摘