胡国胜1,2,任震2,黄雯莹2,万国成2
(1.广东省科技干部学院;广东省 广州市 510640;
2.华南理工大学电力学院;广东省 广州市 510640)
摘 要:对称小波或反对称小波具有线性相位或广义线性相位,因而在信号的分解和重构中非常重要,它可以避免信号失真。在工程中广泛使用的Daubechies小波和Symmlet小波都不是对称小波,作者使用的对称小波构造方法是一种通用的方法,并就Db4和Sym4小波构造了对称小波,构造出的对称小波的计算量是原先小波的一半,提高计算速度。仿真结果表明,由Db4构造的对称小波包与Db4小波包相比,在信号分解与重构过程中具有频率泄漏少、能量集中、计算量小和实时性好等优点。
关键词:Daubechies小波;Symlets小波; 对称小波;小波包;分解与重构
1 引言
Daubechies已经证明除了Harr小波基外,不存在对称的紧支正交小波基[1]。也就是说除了Harr小波外,不存在同时具有紧支、对称、正交的小波。人们针对各种应用领域和目的,构造了不同类型的小波。其中构造对称或反对称的尺度函数和小波函数是非常重要的,因为可以构造紧支的正则小波基,而且具有线性相位。在信号分析中,尺度函数和小波函数又能够作为滤波函数,如果滤波器具有线性相位,则能避免信号在小波分析和重构时失真。
近年来,小波变换在电力系统的故障信号分析与处理中得到广泛的应用[3~6]。文献[3]将B样条小波应用到故障分类与识别;文献[4]针对Morlet小波构造了单向递推快速算法应用于微弱故障的诊断;文献[5][6]将Daubechies小波、Symlets小波、Coiflet小波以及双正交小波应用到电力系统奇异信号的分析和故障诊断中。但它们大多是不对称的,尤其文献[5]用没有线性相位的非对称小波的小波包算法压缩和重构故障信号,很显然影响重构效果。本文就任何不对称的尺度函数和小波函数构造对称的尺度函数和小波函数的方法是一种通用的方法。仿真结果表明Db4构造成的对称小波包比Db4小波包的分解重构效果好得多,它具有减少频率泄漏、能量集中、计算速度快和实时性好的优点。
2 对称小波的构造及性质
众所周知,Daubechies尺度函数Φ(x)和小波函数Ψ(x)具有如下性质:
它的支撑集为[-(N-1),N]。具有时间整数平移正交性,但不具有对称性。
尽管Daubechies小波在工程中得到广泛的应用,但由于其不具有对称性,往往给应用带来不便,下面就从不对称的Daubechies小波构造对称小波。定义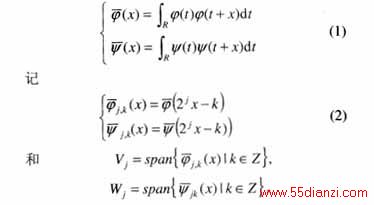


![]()

出;性质3)表明{an}的支撑集长度与{hn}一样,但偶数项系数为零,所以对称小波的计算量减少到原来的一半,计算速度大约提高一倍。从表1中可看出偶数项系数为零,理论分析和实际计算相符。性质3)、性质4)的证明和文[2]相似。
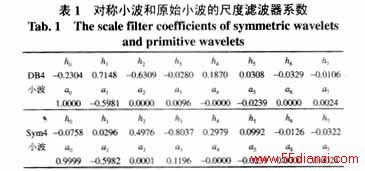
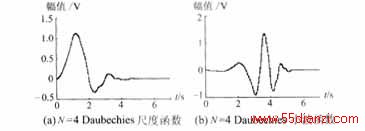
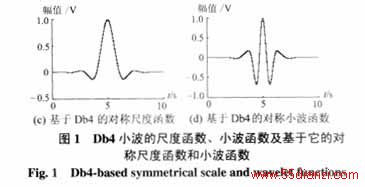
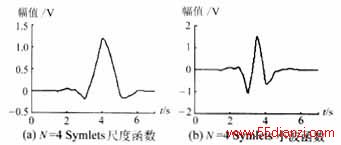
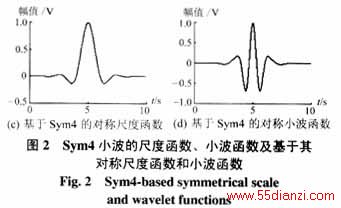
Db4小波和Sym4小波的尺度函数、小波函数及基于它的对称尺度函数和小波函数见图1和图2。
3 对称小波包定子单相接地故障信号分解与重构
基于Daubechies小波构造成的对称小波虽然失去了正交性,但对信号的分解与重构来说,对称性要比正交性更为重要。因为基于对称或反对称的尺度函数和小波函数的滤波具有线性相位或广义线性相位[1],从而避免信号失真。
按图3所示对小波包算法进行了分解和重构。
在图3所示的小波包树分解图中,顶点(0,0)代表原始信号f(t),利用2组滤波器系数{hn}和 {gn},将信号f(t)分解为近似部分和细节部分。其中{hn}为低通滤波器,通过该滤波器作用后得到的信号称为近似部分(低频分量),如图中结点 (1,0)。{gn}为带通滤波器,通过它作用后得到的信号称为细节部分(高频部分),如图中结点(1,1)。此近似部分((1,0)结点)和细节部分((1,1)结点)称为信号f(t)经过小波(包)变换后在尺度1上的表现。然后对近似部分((1,0)结点)和细节部分((1,1)结点)分别进行低通和高通滤波得到尺度2上结点(2,0)、(2,1)、(2,2)和(2,3)。依此类推,在第5尺度上可以得到结(5, i) i=0, 1, 2,…, 31。
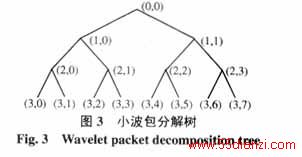
每个结点实质上代表着一定的频率范围。例如,若采样频率为fs,则近似部分为经过{hn}滤波器作用后得到的频率介于[0,fs/4]的分量,而细节部分则为经过滤波器{gn}作用后得到频率介于[fs/4,fs/2] 的分量,即尺度1上的近似部分结点(1,0)代表频率介于[0,fs/4],结点(1,1)代表频率介于[fs/4,fs/2]的分量。同理,尺度2上的结点(2,0)、(2,1)、(2,2)和(2,3)分别代表频率介于[0,fs/8]、[fs/8,fs/4]、[fs/4,3fs/8]和[3fs/8,fs/2]。依此类推,尺度5上各节点[5,i]分别代表频率介于[i.fs/64,(i+1)fs/64],i=0,1,2,...,31。利用最底层的近似部分和各尺度上的细节部分可对原信号进行重构还原。
与Daubechies正交小波包相比,基于本文构造的对称小波的小波包的优点在于分解时,信号的能量相对集中;而重构时可以不失真地恢复原始信号,这点在工程信号处理中是非常重要的。
图4、图5是分别基于Db4小波包和基于Db4构造的对称小波包的某定子单相接地故障A相电流信号分解,信号的采样频率fs=2000Hz,分解层次为5。
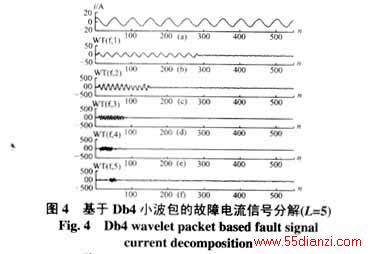
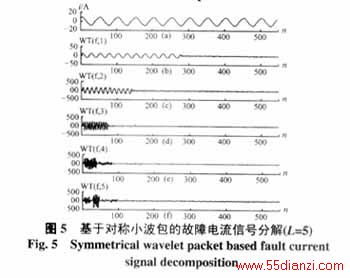
从图4和图5很明显地看出,随着分解层次的增大,基于Db4的小波包分解算法得到的故障信号的能量越来越分散。而相反,基于文中构造的对称小波的小波包算法,它的能量很集中。带来的直接结果是:用对称小波的小波包重构信号时的能量损失要比用Db4小波重构信号时的能量损失小,避免了信号重构时的失真现象。
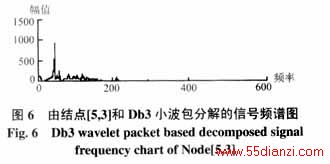
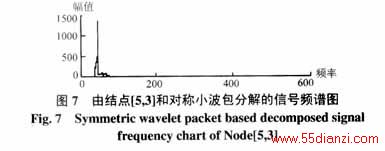
图6、图7是对应于图4和图5结点[5,3]的频谱图,因为采样频率fs=2000Hz,根据前面的结点与频率关系的讨论,可知基频fs=50Hz属于结点(5,3),而频率100Hz属于结点(5,4),这可从图6、图7看出。另外,从图中还可看出,直接由Db4小波构造小波包的重构信号时的频率泄漏严重,能量分散。采用本文的方法先将Db4变换成对称小波,然而用对称小波包重构信号时的频率泄漏要小得多,能量相对比较集中。
为了更好地说明问题,在此引用文[5]中的定义,并根据此定义求得各自的能量恢复系数和相对误差如表2所示。



4 结论
对称小波以及对称小波包具有线性相位或广义线性相位,在信号的分解与重构时可避免信号失真,所以构造对称小波和对称小波包非常必要,本文提出的由非对称小波构造对称小波的方法是一种通用的方法,就非对称小波Db4构造了对称小波。仿真结果表明Db4构造成的对称小波包比Db4小波包的分解重构效果好得多,它具有减少频率泄漏、能量集中、计算速度快和实时性好等优点。
参考文献
[1] Daubechies I.Ten lectures on wavelet[M].Capital City Press,1992.
[2] Fa X,Chao C.Correlation wavelet and its applications[J].Chinese quarterly journal of mathematics,1999,14(1):5-9.
[3] Hong C,Elangovan S.A B-spline wavelet based fault classification scheme for high speed protection relaying[J].Electric mathines and power systems,2000,28(2):313-324.
[4] 何建军,任震,黄雯莹,等(He J J,Ren Z,Huang W Y et al).电力系统突变信号检测的一种实时小波算法(A real time wavelet transform algorithm of sudden changeable electric power system signals detection)[J].中国科学(Sciene in China),2000,30 (1):79-84.
[5] 任震,何建军,黄雯莹,等(Ren Z,He J J,Huang W Y et al).基于小波包算法的电机故障信号的压缩和重构(Compression and Reconstruction for Faults Signals of Motor Based on Wavelet Packets)[J].中国电机工程学报(Proceedings of the CSEE),2001,2(1):25-29.
[6] 管霖,吴国沛,黄雯莹,等(Guan L,Wu G P,Huang W Y et al).小波变换在电力设备故障诊断中的应用研究(Study on the application of wavelet transform in fault diagnosis of electric devices)[J].中国电机工程学报(Proceedings of the CSEE),2000,20(10):46-49,54.
本文关键字:电机 电工文摘,电工技术 - 电工文摘