电力系统故障计算中互感线路的处理

石东源，李银红，段献忠，何仰赞

（华中科技大学电力工程系,湖北 武汉 430074）

    摘  要：在基于节点导纳矩阵的故障计算方法中，由于部分线路间零序互感的存在，使得零序节点导纳矩阵的形成、尤其是互感线路故障情况下零序节点导纳矩阵的形成复杂化。该文对电网中多回互感线路及存在部分互感情况下的等值处理方法进行了统一的数学分析，提出了简便的算法，并在此基础上，对互感线路故障情况下增设节点后故障线路的分解进行了研究，提出了通用的分解规则。该算法和规则对电网中任意重互感线路、任意复杂部分互感结构和互感线路上任意重故障都具有灵活的处理能力，有助于推进电力系统故障计算软件的实用化。
    关键词：电力系统；故障计算；互感线路

1  引言 
    故障计算是电力系统分析计算中的重要内容，在电力系统的运行分析、继电保护整定和设备选择中均需要进行大量快速和精确的故障计算。计算的快速性主要取决于数学模型和算法的选择，而计算的精确性主要依赖于对实际电力系统电网结构的全面合理的数据建模。由于现代电力系统的复杂性，现有的故障计算处理方法和相应的软件产品在对电网进行数据建模时往往做了很多简化，如：忽略电阻、将变压器转化为用线路来表示、忽略线路间的零序互感或仅考虑平行双回线间的全线互感等，从而使得计算结果的精确性受到影响。
    目前电力系统在架设新的输电线路时考虑到输电走廊的问题，平行双回线的架设逐渐增多，而且，由于线路的长短不一以及走线方式的多样化，使线路之间的互感往往只是部分性的，即：一条线路的某一段与其它短线路的全线或长线路的某一段存在互感，这种多回互感线路及线路间复杂部分互感结构的正确描述和处理对计算结果的正确性将产生重要影响。
    在我国，由于三峡电站和西电东送等大型工程的建设，大量电力都将通过多条高压并行线路输送，输电容量巨大，使得线路间零序互感的影响成为一个不容忽略的问题。
    本文以基于节点导纳矩阵的故障计算数学模型为基础，对电网中任意重互感线路、任意复杂部分互感结构和互感线路上任意重故障的处理方法进行了全面的探讨，提出了统一的算法，并在此基础上开发了适用于大型复杂电网的故障分析计算软件。在华中电网中的应用证明，该软件提高了电力系统故障分析计算的水平。
2  故障计算的数学模型和基本算法
    电力系统的故障计算可归结为对故障状态下网络方程的求解，其三序导纳型网络方程为
   

式中  V  (120) 为网络节点三序电压列向量；I (120) 为网络节点三序注入电流列向量；Y (120) 为网络节点三序导纳矩阵。设网络节点数为n，则V (120)和I (120)为3n维向量，Y (120) 为3n×3n维矩阵。
    通常情况下，假设网络元件参数三相对称，则系统正常运行时三序网之间不存在参数耦合关系，可将式（1）写成矩阵形式为

式中  V (0)、I (0)和Y (0)分别对应于式（1）中的V (120 )、I (120) 和Y (120)。
    电网发生故障瞬间，设其网络方程为
    Y(f)V(f)=i(f)            (4)

式中  V (f) 为故障时的网络节点三序电压列向量，I (f) 为故障时的网络节点三序注入电流列向量，Y (f) 为故障时的网络节点三序导纳矩阵。
    因故障瞬间电流不能突变，故I (f)＝I (0)。而导纳矩阵具有可迭加性，故障时的网络节点三序导纳矩阵Y(f)可由正常三序导纳矩阵Y (0)和故障修改导纳矩阵DY (f) 迭加而成，设故障重数为nf，则有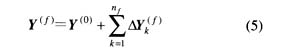

    解线性方程组式(4)，可以求得网络节点三序电压列向量V (f)，由V (f) 和各网络元件的阻抗参数即可求得全网的三序电流分布，进而组合得到故障瞬间全网的三相电压及三相电流。这种基于节点导纳矩阵的故障计算方法其关键在于计算DY (f)，它反映的是故障情况下三序网络之间在短路点或断线口形成的串并联关系。
    但实际上，由于故障情况下往往需要增设节点，式(3)和(5)中的Y (0)并不相等，把式(5)中的Y (0)重新记为Y (f0)，设故障时需要增设的节点数为m，则Y (f0)的维数为3(n+m)×3(n+m)。新节点的出现使得网络结构出现局部的变化，在形成Y (f0)的过程中必须对新增节点所在的线路或变压器进行阻抗参数分解，在互感线路故障的情况下，这种分解包括线路自身零序阻抗参数和线路间互感阻抗参数的分解两部分，从而增加了计算的复杂性。
    可见，Y (f)的形成可以分为2个阶段，首先，根据故障位置增设节点（线路中间短路，新增1个节点，线路中间断线，新增2个节点，母线出口处断线，新增1个节点），形成扩维后的节点导纳矩阵Y (f0)，这一过程与故障参数无关。然后，根据故障类型和参数将相应的故障修改导纳矩阵DY (f)迭加到Y (f0)中对应于该故障的节点上，形成故障时的三序节点导纳矩阵Y (f)。这一过程与第一个过程可以完全独立进行。关于DY (f)的计算已经有系统的方法[1,2]，本文的研究只着眼于第一个过程中互感线路故障情况下增设节点后零序节点导纳矩阵的形成算法。
3  无故障情况下多回互感线路的处理
    常用的互感线路处理方法是采用一种消去互感的等值电路来代替原来的互感线路组，然后就象无互感的网络一样计算零序节点导纳矩阵。
    设互感线路的重数为k，即线路Li（i∈[1,k]），两端节点为pi、qi（i∈[1,k]），零序自阻抗为zi（i∈[1,k]），线路Li与Lj之间的互感为zmij（i∈[1,k]i≠j）。该互感线路组的电压方程为
 

    将式（6）左侧的阻抗矩阵求逆，写成导纳矩阵

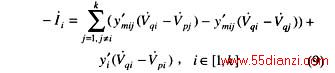
    式(8)、(9)的物理意义为：线路Li的等值导纳变为（≠1/zi），线路Li与Lj的同名端节点pi和pj以及qi和qj之间的等值导纳为-，而异名端节点pi和qj以及qi和pj之间的等值导纳为。由此即可形成互感线路组节点的零序节点导纳矩阵元素。其算法的具体步骤为：
    （1）依次取对角元素（i∈[1,k]），修改与之相关联的两个节点pi和qi的自导纳和互导纳；
    （2）依次取上三角矩阵中的元素（i∈[1,k],j>i），修改pi、qj及qi、pj两组节点的自导纳和互导纳，并用-修改pi、pj以及qi、qj两组节点的自导纳和互导纳。
    对于同杆并架双回线，pi、pj及qi、qj可能是同一个节点，在算法中需要进行节点合并。
    以上讨论的是线路之间的互感遍布全线均匀分布的情况，但在实际系统中，线路之间往往只是部分存在互感，下面以图1所示的三回互感线路组为例分析之。线路L1全线与线路L2的0%~40%段存在互感zm12，而线路L3全线与线路L2的60%~ 100%段存在互感zm23，在该互感线路组无故障运行状态下，无论线路之间部分互感怎么分布，线路两端节点的电压和线路电流始终满足式(6)，即：

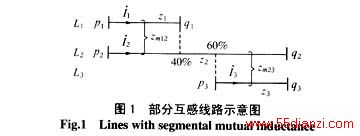
它和线路L1与线路L2的全线存在互感zm12以及线路L3与线路L2的全线存在互感zm23的情况是完全等价的，对零序节点导纳矩阵的形成毫无影响。
4  互感线路故障情况下的分解
    故障时需在故障位置增设节点，导致了网络结构的变化，如图2。无互感线路L在距离p节点40%处短路时需增加节点r，线路L被分解为两条线路pr和rq，两线路的阻抗按比例分配为：zpr=2z/d,zrq=3z/5。这种分解只影响故障线路。

    而对于互感线路，由于它与其他线路存在耦合关系，采用第3节中的等值处理方法，新增节点也与属于该互感组的其他线路的节点之间存在耦合导纳。所以，处理互感线路故障时，既需要象无互感线路一样将故障线路的零序阻抗按比例分解到故障新增节点两侧的线路上去，也需要将互感参数按比例分解，并且要保持正确的互感范围关系，以保证对多重复杂故障的正确处理。
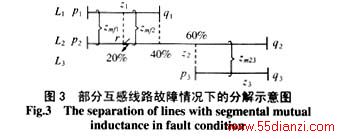
    仍以图1中的3回互感线路组为例，设在线路L2上距离p2节点20%处发生短路，短路点设为r，故障后的状态如图3所示。线路p2r和rq2的零序阻抗按比例计算得：zp2r=z2/5,zrq2=4z2/5 ,由于故障点位于线路L2与L1的互感段内，所以zm12需要分解为两部分，其一为线路L1的0%～50%段与线路p2r全线的互感，互感阻抗为zmf1=zm12/2；其二则为线路L1的50%～100%段与线路rq2的0%～25%段的部分互感，互感阻抗为zmf2=zm12/2。线路L2的60%～100%段与线路L3全线的互感则由于短路点不在该范围内而不需要分解，但应转化为线路rq2的50%～100%段与线路L3全线的互感。这样分解以后，即可把新的互感线路组看成由线路L1、p2r、rq2和L3等4条线路组成，而且他们两两之间的互感可以不用考虑部分互感范围的因素，而是当成全线互感,按照式(6)～(9)的原理来处理。
    考虑任意重互感组和任意复杂部分互感结构的情况，设互感线路的重数为k，线路Li（两端节点为pi、qi）的bi%～ei%段与线路Lj（两端节点为pj、qj）的bj%～ej%段存在互感zmij，其中，bi，ei，bj

>,ej∈[0,100] ei> bi,ej>bj,ij∈[1,k]。设线路Li上的fi%（0<fi<100）位置发生短路故障，新增节点ri，则zmij的分解规则为
    （1）如果bi<fi<ei,如图4(a)所示，则线路piri的(100)bi/fi)%～100%段与线路Lj的

    对于互感线路组内多处故障，甚至是一条线路上多处故障的情况，均可按照以上规则对每一故障及其新增节点依次处理，每处理一个新增节点，互感组的重数增加一重，后续新增节点的处理针对重数增加后的互感线路组进行。其中对于一条互感线路内多处故障的情况，后处理的故障应根据先处理的故障产生的新线路进行相应的调整。如对于图5所示的情况，线路L2在距离p2节点f1%和f2%位置发生故障，先对f1%位置故障的新增节点r1进行分解处理后，f2%位置的故障应相应调整为线路r1q2上距离r1节点[100(f2-f1)]/(100-f1)%位置的故障。

5  结论
    在故障计算中，对互感线路的处理是比较复杂的部分，尤其是在多回互感线路组中存在部分互感且故障发生在互感线路上的情况。本文探讨了无故障情况下互感线路的等值处理方法和计算机算法及故障情况下互感线路的分解，提出了一种统一的分解规则和算法，对于电网中任意重互感线路、任意复杂部分互感结构和互感线路上任意重故障都具有灵活的处理能力，有助于推进电力系统故障计算软件的实用化。

参考文献

[1]  陈亚民（Chen Yamin）．电力系统计算程序及其实现（Power System Calculation Programs and Their Implementation）[M]．北京：中国电力出版社（Beijing：China Electrical Power Press），1995．
[2]  王春，陈允平，谈顺涛（Wang Chun，Chen Yunping，Tan Shuntao）．电力系统复杂故障计算通用算法的研究（The Study of Generalized Algorithm for Simultaneous Faults in Power Systems）[J]．中国电机工程学报（Proceedings of the CSEE），1995，15(6)：418-422．

本文关键字：暂无联系方式电工文摘，电工技术 - 电工文摘