摘 要:配电网中发生最多的是单相接地故障,因此如何快速准确的检测出接地故障点成为小电流接地系统实现配电自动化的一个重要研究课题。在分析了小电流接地系统发生单相接地故障暂态特征的基础上,提出了运用连续小波变换分析暂态零序电流中的高次谐波分量,实现故障选线的方法。通过仿真分析,证明了该方法的灵敏性和可靠性。
关键词:小电流接地系统;单相接地故障;故障选线;连续小波变换; Prony方法
1 引言
我国35KV及以下电压等级的配电网中性点一般采用不接地或经消弧线圈接地方式,因其发生接地故障时,流过接地点的电流小,所以被称为小电流接地系统。据电力运行部门的故障统计,小电流接地系统中单相接地故障发生率最高,约占总数的80%。小电流接地系统发生单相接地故障时不形成短路回路,只是经线路对地电容形成较小电流通路,电网线电压仍然对称,允许维持运行一段时间。但是发生单相接地后,非故障相电压升高为线电压,而且间歇性弧光接地可能引起电弧接地过电压,对系统绝缘有威胁,容易扩大为相间短路,因此应尽快查找故障位置,清除故障【1】。
系统发生接地故障时,故障信号中含有重要的暂态分量,传统的信号分析方法如快速傅立叶变换FFT、卡尔曼滤波、最小方差法和有限脉冲响应滤波等对于分析暂态信号都存在着局限性。小波变换是分析非平稳信号,提取信号暂态特征的一种有效的信号处理方法。它克服了傅立叶变换不能对信号同时进行时频局部化分析的缺点,可以对信号进行精细分析,特别是对暂态突变信号或微弱信号的变化较敏感,能够提取暂态信号中各个频段分量加以分析。所以近年来被广泛应用于各个领域。
本文把连续小波变换引入小电流接地系统单相接地故障选线中。利用连续小波变换提取故障信号中暂态分量的有用信息,以变换后的小波系数构成选线判据。通过EMTP仿真分析,证明该方法具有很好的灵敏性和可靠性。
2 故障特性及保护【1】
在中性点不接地电网中发生单相接地故障时,由于故障线路零序电流的大小等于所有非故障线路的零序电流的大小之和,故障线路的零序电流与非故障线路的零序电流相位相差1800,即故障线路的零序电流与非故障线路的零序电流相位相反。所以采用反应基频稳态分量的零序电流保护和零序功率方向保护就可以取得满意的效果。
在中性点经消弧线圈接地的电网中发生单相接地故障时,在系统普遍采用的消弧线圈过补偿方式下,故障线路的零序电流与非故障线路的零序电流大小相差不大,相位一致,所以不能采用反应基频稳态分量的零序电流保护和零序功率方向保护。由于对谐波分量来说,消弧线圈接地电网的特性相当于中性点不接地电网的特性,如同中性点不接地电网一样,故障线路零序电流的谐波分量,与非故障线路零序电流的谐波分量之间相位相差1800,即相位相反,故障线路零序电流的谐波分量的大小远远大于非故障线路零序电流的谐波分量的大小,所以可以利用零序电流保护和零序功率方向保护原理,构成反应谐波分量的零序电流保护和零序功率方向保护。
3 故障暂态量的连续小波变换
由于暂态分量成分复杂而且衰减快,持续时间短,因此为了完整有效的提取暂态分量,文中采用了素有分析信号的数学显微镜之称的小波变换。小波变换在时频两域都具有表征信号局部特征的能力,在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分,所以被誉为分析信号的显微镜。
小波变换又大体分为连续小波变换、离散小波变换和基于多分辨率分析思想的正交小波变换。连续小波变换的小波变换系数具有很大的冗余性,利用连续小波变换进行动态系统故障特征提取不容易丢失信息,因此连续小波变换被广泛应用于时频联合分析、去噪、特征提取等领域【2】。利用连续小波变换进行动态系统故障检测与诊断具有良好的效果。但是连续小波变换的缺点是计算量很大,对硬件设备的要求(A/D芯片的转换速度,RAM的存储量、CPU的计算速度等)较高,不利于实际应用。
本文选用一个具有很好的对称性、紧支集和正则性的复数函数【3】作为连续小波母函数来提取暂态信息,可以保证不丢失瞬间消失的暂态信息量。同时,为了减少连续小波变换系数的计算量,以利于实际应用,本文在计算小波变换系数时运用变换的方法来代替传统连续小波变换系数计算中的内积计算【3】,有效的减少了计算量。
本文选用的复数母小波是
![]()
其中设wo=2π,以使1/a=f;设![]() 以使Ψ(t)满足可容许性条件。它的时域和频域的波形如图1所示。
以使Ψ(t)满足可容许性条件。它的时域和频域的波形如图1所示。


设信号为s(t),对于某个频率f和采样点kT的小波变换系数就可以表示为:
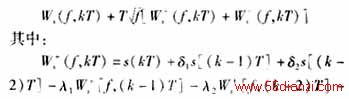
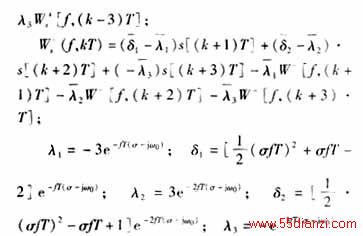
对于某个频率f,用这种算法计算一个的小波变换系数需要计算36次实时乘法和35次实时加法;那么如果对信号进行N次采样,并且要分析nf个频率,那么总的计算量就是36nfN。这大大减少了小波变换系数的计算量。
4 基于连续小波变换的选线方法
本文的选线方法是以零序电流某高次谐波的连续小波变换系数的相对相位法为主要判据;以各馈线零序电流某高次谐波的连续小波变换系数的幅值同母线零序电压同次谐波的连续小波变换系数的幅值比较作为辅助判据。即主判据是故障馈线的零序电流某高次谐波的连续小波变换系数的相位与非故障馈线的零序电流同次谐波的连续小波变换系数的相位相反;辅判据是![]() ,其中K值的选取根据具体的电网而定。
,其中K值的选取根据具体的电网而定。
5 Prony方法【4】
在基于连续小波变换的选线方法中,计算小波变换系数Wij(f,kT)和Wu(f,kT)时需要确定计算的频率f,本文应用Prony方法【4】来确定这个频率。Prony方法是分析中性点经消弧线圈接地系统中,发生单相接地故障或两相短路接地故障时的接地电流的有效工具,是一种用来估算信号中存在的各个形式分量的技术。Prony方法将信号中存在的每个分量都用四个参数(频率、衰减因子a、幅值A和相角θ)来表示。
在一个中性点经消弧线圈接地系统中发生单相接地故障时,设接地电流为x(t),假设电网中非线性动态分量可以忽略,x(t)就可以表示为按指数衰减的正弦函数之和:
![]()
其中q是函数的个数,Ak代表幅值,ak是衰减因子,fk是以赫兹为单位的频率,θk是以弧度为单位的相角。对衰减的指数分量来说,fk=0,θk=0或π。对于不衰减的正弦分量来说,ak=0。设x(t)由q1个衰减的指数分量和q2个不衰减或按指数衰减的正弦分量组成,q=q1+q2。
Prony方法还可以应用到对故障馈线的零序电流、零序电压和非故障馈线的零序电流的分析中。在同一个电网中,对故障相的接地电流进行分析的结果和对故障馈线的零序电流、零序电压以及非故障馈线的零序电流进行分析的结果是一样的。在本文应用中只需分析其中之一就可以了,下文的仿真中选择分析故障馈线的零序电流。
本文中应用Prony方法是为了确定计算故障信号中的暂态高频分量的小波变换系数时的频率。因此在应用Prony方法的计算结果中,主要考虑按指数衰减的正弦分量,即故障信号中的暂态高频谐波分量;在计算出的几个按指数衰减的正弦分量的频率中选择一个合适的频率作为小波变换系数的计算频率。
6 仿真分析
下面通过电磁暂态仿真程序EMTP针对一个10KV配电网,来验证这种选线方法的主判据。
图2所示是一个辐射形的10KV配电网,中性点经消弧线圈接地。母线外接5条馈线。图中各条馈线的长度L1—L5可以是不等的,D为故障点距母线的距离。Rd为接地故障阻抗。线路及变压器参数与实际情况相符。
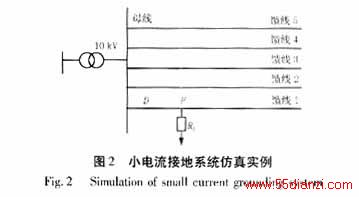
为了验证本文提出的用连续小波变换提取暂态信息实现小电流接地电网单相接地故障选线的方法,作了大量的EMTP仿真。在图2所示的电网中,针对馈线1上不同的故障点(故障点距离母线的长度不同),不同的接地阻抗值,不同的馈线1和馈线2的长度,在母线上的故障,以及瞬间故障都作了仿真。限于篇幅,只给出两个仿真实例。
当改变图2示电网中的参数(故障点距母线的距离、所有馈线的长度和、接地阻抗的值)时,对故障馈线上的零序电流应用Prony方法总可以得出,p=7,q=4。信号中包含四个分量:两个指数衰减的正弦分量EDS1和EDS2,一个衰减的指数分量DE和一个基频正弦分量PS。在EDS1和EDS2的频率和之间选择一个作为计算小波变换系数的频率。因为Prony方法需要较高的采样率,为了兼顾选线的准确度和对硬件的要求,本文选用4000HZ作为故障检测的采样率。
实例1.假设馈线1和馈线2的长度相同,即L1=L2=20km,馈线总长度为L=125km,其中L3=15km,L4=10km,L5=30km.在馈线1上距母线D=10km的F点处发生单相接地故障,接地阻抗Rd=5Ω。故障发生在馈线1的A相相电压的相位角为300时。故障馈线的零序电流如图3所示:
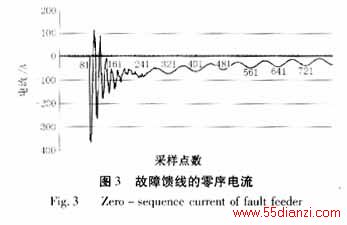
根据Prony方法,故障馈线1上的零序电流包含以下形式的分量:两个按指数衰减的正弦分量EDS1和EDS2,一个基频正弦分量PS,还有一个衰减的指数分量DE。因此,故障馈线上的零序电流就可以被表示为:
表1列出了每个分量的四个参数值:
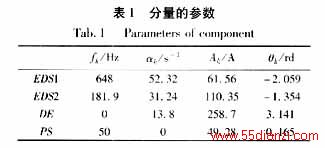
由表中数据,按指数衰减的正弦分量EDS1和EDS2的频率分别为f1=648Hz,f2=181.9Hz。在中性点经消弧线圈接地系统中,显然频率f2=181.9Hz的分量EDS2受消弧线圈的影响较大,不宜将f2=181.9Hz作为计算频率。选择f1=648Hz作为计算频率,结果证明不受消弧线圈的影响。
使用小波变换观察故障时各条馈线上零序电流和母线零序电压的谐波分量,需要确定观察窗口的宽度(大小)。本文使用一个宽度为9ms的分析窗口。为了不受边界效应的影响,我们不考虑窗口开始3ms和结束3ms的小波变换系数,只保留位于分析窗口中间3ms的小波变换系数。
图4给出了非故障馈线2的零序电流中频率f=648Hz的分量的小波变换系数相角c1随时间的变化曲线,和故障馈线1的零序电流中频率的分量的小波变换系数相角 c2随时间的变化曲线。
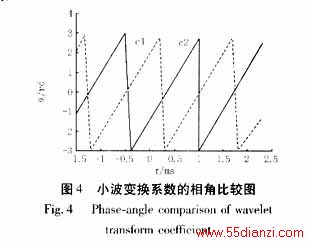
从图中我们不难看出仿真的结果和理论分析的结论是一致的,即非故障馈线零序电流的频率f=648Hz的小波变换系数的相角和故障馈线零序电流的频率f=648Hz的小波变换系数的相角相位相反。
实例2.设L1=L2=20km,其余馈线长度不变,馈线总长也不变。馈线1上在距母线处,发生接地阻抗的单相接地阻抗Rd=8Ω故障。故障发生在馈线1的a相相电压的相位角为30°时。
在这个例子中对故障馈线的零序电流应用Prony方法算得的按指数衰减的正弦分量EDS1和EDS2的频率分别为f1=739Hz,f2=317.5Hz。显然应当计算f=739Hz的小波变换系数的相角。
图5给出了非故障馈线2的零序电流中频率f=739Hz的分量的小波变换系数相角c1随时间的变化曲线,和故障馈线1的零序电流中频率的分量的小波变换系数相角c2随时间的变化曲线。
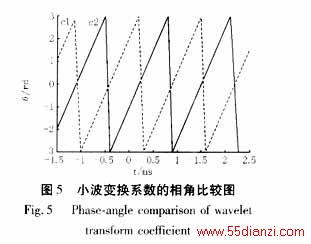
这个例子的仿真结果再一次证实了本文所提出的选线方法的可靠性。
6 结论
本文在分析了中性点不接地电网和中性点经消弧线圈接地电网中发生单相接地故障时的稳态和暂态特征的基础上,以充分提取故障信号暂态信息为出发点,利用连续小波变换系数有很大的冗余度,适合用于动态系统的特征提取的优点,选用了一个具有很好的对称性、紧支集和正则性的复数函数作为连续小波母函数来提取故障后的暂态信息。
本文的选线方法是以零序电流某高次谐波的连续小波变换系数的相对相位法为主要判据,以各馈线零序电流某高次谐波的连续小波变换系数的幅值同母线零序电压同次谐波的连续小波变换系数的幅值比较作为辅助判据。
为了克服连续小波变换计算量大,不利于实际应用的缺点,本文用Z变换代替了传统的连续小波变换系数计算中使用的内积的离散计算,大大的减少了计算量。应用本文所提出的方法计算连续小波变换系数时需要确定所要计算的频率,本文应用Prony方法来确定这个频率。
用Prony方法计算故障馈线的零序电流或零序电压,或者非故障馈线的零序电流得到的分量数与所计算电网的参数(故障点距母线的距离、馈线的总长度、接地阻抗的值)有关。但是对于一个给定的电网,分量数是确定的,故障情况的不同不会影响分量数;因此,信号中的按指数衰减的分量数也是确定的。按指数衰减的正弦分量的几个频率中,通常都不选择最低频率作为计算频率,因为有时最低的频率太低,受消弧线圈影响较大;有时受故障情况(例如接地阻抗大小)的影响较大【4】。因此通常选择较高频率或最高频率作为计算频率。总之,在各种网络情况下发生单相接地故障时,应用此算法计算小波变换系数时的最优频率选取问题需要根据具体情况来确定。
本文在一个10KV的中性点经消弧线圈接地的电网中,对各种故障情况作了大量的仿真实验,充分验证了该选线方法主判据的灵敏性和可靠性。
参考文献
[1] 张志竟,黄玉铮合编. 电力系统继电保护原理与运行分析(上册). 北京:水利电力出版社,1995,11.
[2] 彭玉华著. 小波变换与工程应用. 北京:科学出版社,1999.
[3] Chaari O,Meunier M,Brouaye F. Wavelet: a new tool for the resonant grounded power distribution systems relaying. IEEE Trans.on Power Delivery,Vol.11,No.3,July 1996: 1301-1308.
[4] O.Chaari, P.Bostard and M.Meunier. Prony's method: an efficient tool for the analysis of earth fault currents in Peterson-coil-protected networks. IEEE PES Winter Meeting,New York,Jan/Feb,1995: 1238-1241.
本文关键字:暂无联系方式电工文摘,电工技术 - 电工文摘