一种滤除衰减直流分量的快速算法

摘　要：针对全周傅氏算法在处理含有衰减直流分量的周期信号时将会产生误差的问题，本文在全周傅氏算法的基础上提出了一种滤除衰减直流分量的快速算法，仅增加一个采样点，进行两次全周傅氏变换，经过理论推导，得到各周期分量的精确计算公式。并通过仿真证实，此算法具有速度快，精度高的特点。
　　关键词：衰减直流分量；全波傅氏算法；快速算法

A FAST ALGORITHM FOR FILTRATING DECAYING DC COMPONENT

Hou Youtao Zhang Ju

(North China Electric Power University, Baoding, 071003)

　　Abstract: To solve the problem that the full-wave Fourier algorithm will bring errors when there is decaying DC component in the sampling signal, this paper gives a new fast algorithm based on the full-wave Fourier algorithm which can filtrate the decaying DC component by adding only one sampling point with two full-wave Fourier transforms. The precise calculation formula can be deduced theoretically, and the characteristics can be proved by simulation.
　　Key words: decaying DC component; full-wave Fourier algorithm; fast algorithm


0 引言
　　电力系统发生故障时，故障信号中除了基波分量以外还含有大量的高频分量和衰减的非周期分量。在微机保护中，通过相关算法对信号进行处理，得到基波或某次谐波分量的数值来实现故障检测功能。微机保护算法的计算可视为对交流采样信号中参数的估算过程，对算法性能的评价也取决于其是否能在较短数据窗内，从信号的若干采样值中提取出有用成分。传统的全周傅氏算法有很强的滤波能力。能够滤除周期信号中的整数次谐波分量和直流分量。但是，如果采样信号中存在衰减直流分量，其滤波效果就会受到影响。导致基波分量（或某次谐波分量）的计算产生误差。
　　文献【1】提出了在全周傅氏算法基础上通过延长数据窗来滤除衰减直流分量，延长的数据窗为，数据窗过长。特别是在计算基波幅值时，需要的数据窗为，不利于微机保护的快速动作。
　　因此，必须寻求一种数据窗短而精度又高的算法来有效滤除衰减的直流分量，进而精确的求出周期分量的估计值，保证微机保护的快速正确动作。本文提出了一种快速算法，在全周傅氏变换的基础上，采用追加一个采样点的方法，便可消除衰减直流分量的影响。

1 传统的全周傅氏算法
　　假定被采样信号具有如下形式：
　　
式中I0为衰减直流分量初值；T为衰减时间常数，Im(n)和φn分别为n次谐波的幅值和初相角。
　　各次谐波的实部和虚部的时域表达式为：
　　


当式（1）中不含有衰减直流分量时，得到的Im(n)和φn是真实值。以上即为全周傅氏算法的全过程，是基于被采样信号为周期信号的前提下进行推导的，而对于式（1）中存在衰减直流分量的情况再用全周傅氏算法进行计算，则会产生误差，分析如下：


其中：A和B为信号中基波和各次谐波分量通过全周傅氏算法得到的实部和虚部，即理想值，δa和δb为衰减直流分量通过全周傅氏算法得到的值，也就是实际值与理想值之间的误差。为了保证全周傅氏算法在这种情况下仍然具有很好的计算精度，必须对全周傅氏算法加以改进，以消除δa和δb的影响。

2 快速算法
2.1 衰减时间常数的求取
将式（1）离散化可得：

　
　
所以T=-△T/1nr。
2.2快速算法
取t∈[△T,T △T]，即将第一个采样点去掉，在最后补上一个采样点，此时采样序列从2到N＋1，再对进行全周傅氏变换，可得
　
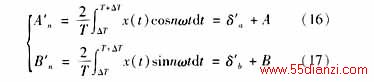
对于信号中的周期分量来说，在[0,T]和［△T,T △T］内的全周傅氏变换结果是相同的。令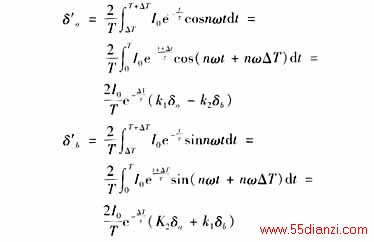

　　

[1] [2]  下一页

本文关键字：暂无联系方式经验交流，电工技术 - 经验交流