线性电路分析——支路法详析

电路的基石是支路。支路电流与支路电压是电路分析与求解的基本对象。当支路电流与支路电压求得后，支路功率（吸收的或发出的）也就可迎刃而解。
支路法的内容有三：
    一.支路电流-支路电压法（简称2b法）
     1．定义：设电路有n个节点b条支路。直接以b个支路电流和b个支路电压作为待求变量，依据KCL、KVL和支路的伏安关系，对电路列写出独立的KCL方程、KVL方程和支路伏安方程而进行求解的一种方法。
     2．电路独立方程的列写：由于电路有b个支路，需要求出b个支路电流和b个支路电压，因而就需要列出2b个独立方程。我们以图3-2-1电路为例来说明2b个独立方程的列写原则和方法。该电路共有六条支路（将电流源is2与电阻R2的并联组合视为一条支路），四个节点，三个网孔，七个回路。设六条支路电流的大小和参考方向如图中所示（支路电压的参考极性均设定为与支路电流的参考方向关联）。根据KCL，对四个节点可列写出四个KCL约束方程：
   　

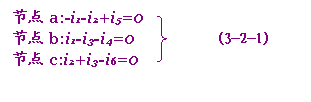
显然着这三个方程是相互独立的，因为其中的任一个都不能从其余两个相加而得到。同理，对节点d可列出:

   i4-i5+i6=0
显然这个方程是不独立的，因为将式（3-2-1）中的三个方程相加既得到它。故可得到结论：对具有四个节点的电路，只能列写出三个独立的KCL约束方程。我们把能列写出独立的KCL约束方程的节点成为独立节点。可见，具有色个节点的电路，只能有且一定有三个独立节点。推广之，具有n个节点的电路，只能有且一定有(n-1)个独立节点，余下的一个节点即为非独立节点。至于选哪些节点作为独立节点，原则上是任意的。例如在图3-2-1电路中，若选节点a,b,c为独立节点，则是（3-2-1）即为三个独立的KCL约束方程。

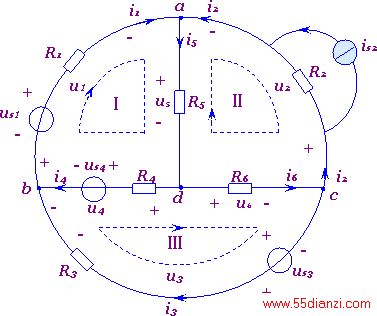
     图3-2-1  复杂电路举例

   图3-2-1共有七个回路，故可列出七个回路KVL约束方程。例如对三个网孔，若选它们的循行方向均为顺时针方向，如图中所示，则可列出KVL约束方程为：
  网孔回路Ⅰ:  u1+u4+u5=0
  网孔回路Ⅱ:  -u2-u5-u6=0　　（3-2-2）      　

  网孔回路Ⅲ:  u3-u4+u6=0
显然，这三个方程是互相独立的，因为其中任一个都不能从其余两个相加得。但若再对其余四个回路中的任一个，譬如外网孔（循行方向也取为顺时针）列KVL约束方程，则有：

  u1-u2+u3=0
    显然，这个方程是不独立的。因为将式（3-2-2）中的三式相加即得此方程。同理，若再取别的一个回路，则所列出的方程也一定是不独立的。故可得到结论：对平面的电路列出的KVL约束方程，其独立方程的个数正好等于网孔的个数。我们把能列出独立KVL约束方程的回路称为独立回路。平面电路中的网孔即为一组独立回路。式（3-2-2）即为图3-2-1电路三个独立KVL约束方程。
    现在的问题是，选什么样的回路才能保证是独立回路，我们在此给出两个结论：（1）.若每选取一个回路，至少包含有一条别的已选过的回路中所没有的支路，则此回路必是独立回路；（2）.平面电路中的网孔必是独立回路。通常为了简便，就直接选取网孔作为独立回路。一个电路有几个网孔，则就有几个独立回路。
图3-2-1的支路伏安方程为：

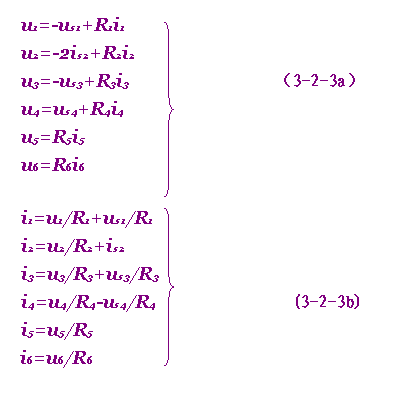
    该电路共有12个待求变量（6个支路电流和6个支路电压）。现在由式（3-2-1）、（3-2-2）、（3-2-3a）或式(3-2-3b)，共得12个独立方程，联立求解即得全部的支路电流和支路电压。
    推广之，对于一个具有b条支路、n个节点的电路，根据KCL可列出（n-1）个独立的KCL约束方程，根据KVL可列出[b-(n-1)]个独立的KVL约束方程，根据支路的伏安关系可列出b个独立的支路伏安方程，这样共可列出[(n-1)+b-(n-1)+b]=2b个独立方程，而待求的变量也是2b个（b个支路电流和b个支路电压），故又称这种方法为2b方程法，简称2b法。联立求解2b个独立方程，即可求得全部的支路电流和支路电压。

需要指出，2b个方程是独立的，2b个变量是完备的，但2b个变量并不是独立的，因为b个支路电流之间要受KCL的约束，b个支路电压之间要受KVL的约束，支路电流和支路电压之间要受支路伏安方程的约束。

二． 支路电流法
    因为支路电压与支流电流之间要受伏安方程的约束，所以若将支路电压变量直接用支路电流变量表示，即可减少b个方程。直接以b个支路电流作为待求变量，依据KCL和KVL列方程，而对电路进行分析的方法，称为支路电流法。
    例如对图3-2-1电路，将式（3-2-3a）代入式（3-2-2）即有:

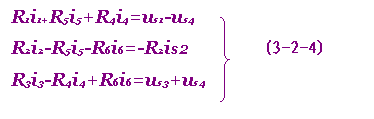
　　此式即为用支路电流表示的网孔KVL约束方程。其物理意义是：在每一个回路中，支路电流在支路电阻上产生的电压的代数和，等于该回路中所有电压源电压升高的代数和（R2is2即为由R2与is2组成的电流源的等效电压源的电压）。式（3-2-4）可直观写出：凡支路电流参考方向与网孔的循行方向一致者，等号左端的项前面取"+"号，否则取"-"号；凡电压源的级性从"-"到"+"与网孔的循行方向一致者，等号右端的项前面取"+"号，否则取"-"号。
    联立求解式（3-2-1）和式（3-2-4），即可得b个支路电流。然后再将所求得的b个支路电流代入式（3-2-3a），即得b个支路电压。
    同样要指出，b个支路电流变量是完备的，但不是独立的，因为b个支路电流之间要受KCL的约束。
    支路电流法的步骤如下：
   （1）.画出电路图；
   （2）.设定各支路电流的大小和参考方向；
   （3）.选取（n-1）个独立节点，列写出(n-1)个KCL约束方程；
   （4）.选网孔为独立回路，并设定网孔的循行方向，列写出网孔的KVL约束方程；

[1] [2]  下一页