的模近似相等的情况，再仅用一项
就有可能给主导低频振荡模式的鉴别带来误差。为此本文对式(11) 作了如下修正：
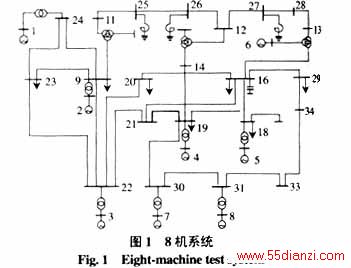
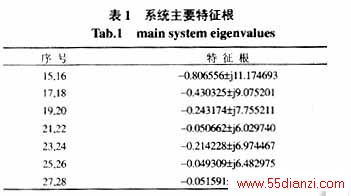
为说明本文提出的ND算法的有效性，对上述系统计算海森矩阵，再求出非线性正则变换系数，在此列出其前6个元素：
再用解析方法求得海森矩阵，进而求得非线性正则变换系数，其对应的前6个元素为：
-0.00942869069496-j0.000360394117736
0.00340272976985+j0.00030146649439
两者各元素的前10位数字是一样的，仅后3位数字有误差，个别的后4位数字有误差，与第3节中的分析是相同的。用非线性正则变换系数的其它元素来比较，结果也是如此，14位数字中也仅后4位数字有误差。对文[7]所示的3机系统，文[8] 所示的单机系统，计算非线性正则变换系数的结果也同样。由此可见本文所提ND算法的有效性。
按本文所提算法算得主导低频振荡模式是λ21 和λ22 , 若仅按式(11)计算，主导低频振荡模式应是λ27 和λ28 。由特征根和状态变量的线性相关因子计算知，这对模式与δ1 线性强相关，也就是与第7台发电机线性强相关。由特征根和状态变量的非线性相关因子[2,4]计算知，这对模式与w1 非线性强相关，同样也是与第7台发电机非线性强相关。同时按文[2]、[4]提出的方法求得模式21与模式22，40(或模式22与模式21，40)间的非线性相互作用最大，这里,
算知，模式40与e'q,6非线性强相关。也就是说，在当前的大干扰下，由于主导低频振荡模式21和模式40间强烈的非线性相互作用，使得7号发电机和6号发电机间也将发生强烈的非线性相互作用。换句话说，节点30处发生短路故障，7号机受到的影响最大，远离故障的6号发电机受到的影响应该较小。但由于主导低频振荡模式21与模式40间强烈的非线性相关作用，进而与6号发电机状态变量间强烈的非线性相关作用的结果，使得远离故障的6号发电机也将受到较大的扰动。
用文[2]中提出的非线性正则变换系数对系统参数的灵敏度思想同样可以说明这一特性。按文[2]中的式(16)，用本文提出的数值微商算法求取
对所有励磁系统参数的灵敏度，得模最大的是相对第8号机励磁系统放大系数Kt8 的灵敏度，为1.18∠68.4 ，次之为相对于第6号机励磁系统放大系数Kt6 的灵敏度，为1.09∠46.7
本文关键字：暂无联系方式电工技术，电工技术 - 电工技术
