
![]()
式中 ispk为电流峰值;is0为消除高频谐波后的低频电流;△iL为电流开关纹波峰的峰值。因积分时间常数误差和电流开关纹波的存在,双路控制方程将修正为
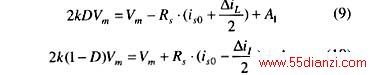
新策略的一个关键问题在于如何取得合适的补偿信号A1、A2,使修正后的控制方程与理想方程基本一致,从而实现网侧电流波形跟踪电压波的目标。
对于单路控制电路,用电流直流分量的负反馈可将直流分量调至零[5]。但考虑到电路稳定性的需要,双向互补策略采用双路切换控制。假设1路控制工作电流正半波,那么由2路控制的电流负半波无法反映1路控制的情况,反之亦然。此时仅由直流分量反馈无法同时对两路控制进行调节,过渡将出现交越失真。
解决交越失真问题,可由两路控制信号之差的负反馈实现。
因两路控制对称且共用一个积分电路,而积分器计算的分别为开关信号的高、低电平时间,积分时间常数误差和电流开关纹波影响将使两路控制信号出现对称性误差,即开关占空比分别偏大和偏小。这将直接影响主电路上进线电流,交越失真即由此引起。若以两路控制信号之差的积分作为负反馈,稳态时可将两路信号调至一致,实现平滑过渡。
考虑到残留直流分量问题,还需引入电流积分反馈。当积分时间常数大于工频周期时,此反馈信号即可体现进线电流直流分量,稳态情况下将直流分量调至零。
双向互补控制的具体做法就是将两路信号之差与电流积分之和作为反馈,同时对交越失真和直流分量进行调整,通过闭环措施将两路控制均调至与理想情况基本相符。图5即为反馈补偿的示意图,其中is为主电路进线电流,D1和D2分别为两路控制的开关占空比。

图6为采用双向互补控制的UCI-APF,两路控制均采用上文介绍的反馈方法。A由电流is积分得到,积分时间常数大于电网50Hz波形的周期。稳态情况下两路控制均可实现网侧电流跟踪电压波,两路切换工作可增加电路的稳定工作范围,而无需增加采样通道。

5 实验与结果讨论
为验证双向互补控制的可行性,按图6进行了实验,其中非线性负载结构为整流桥后带RC负载。电容C为68mF,负载电阻R为270W。交流输入电压为200V,有源滤波器直流侧电压为355V。主回路上电流采样电阻为0.5 W。实验电路中按常规在非线性负载上并联了小电容以吸收本APF的高频开关纹波,本次实验中该电容为2mF。
图7为实验结果,其中图(a)、(b)、(c)分别为不同情况下的网侧进线电流波形。
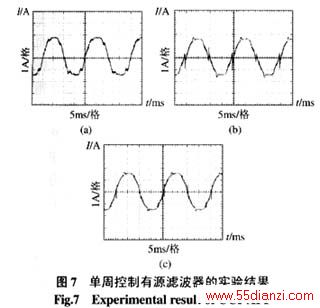
图7(a)为单路控制的电流波形。可以发现,由于积分时间常数及高频开关纹波影响,电流存在明显的直流分量与低频次谐波。滤波器受到本身原理及积分时间常数漂移影响,稳定工作范围有限。
图7(b)、(c)的电流波形均由双路控制得到,系统稳定性提高且降低了直流分量。其中图7(b)仅采用电流积分反馈,两路切换工作时出现交越失真。图7(c)电流波形由本文所提的双向互补控制得到,由波形可看出正负半波对称,降低了直流分量及低频次谐波,且波形稳定,不随参数误差变化而变化。不难发现,采用新策略的反馈方式后,两路过渡的交越失真明显减少。
谐波分析的结果为:网侧输入电压THD为6.9%,谐波负载电流THD为70.2%,图7(c)所示的补偿后网侧电流THD为8.5%。若网侧电压谐波降低,则补偿效果可以更好。
6 结论
本文介绍了一种新型UCI-APF的双向互补策略,即利用双路切换控制这一新概念提高系统稳定性。两路信号之差与电流积分的负反馈改善了以往单周控制所存在的网侧直流分量缺陷,并解决了两路控制切换的平滑过渡问题。实验初步验证了该方案的可行性。双向互补控制无需增加采样通道,易于实现,因此具有很好的发展前景。该电路在细节上的进一步完善还有许多工作要做。
本文关键字:滤波器 电工技术,电工技术 - 电工技术