基于Park矢量模平方函数的异步电动机转子故障检测方法研究

1  引言
    异步电动机以其结构简单、使用寿命长,维护工作方便而在传动领域占有极其重要的地位。对异步电动机进行在线状态监测及时发现异步电机的早期异常，避免电机失效和高价维修，防止产量下降及其带来的经济损失，具有重要的意义。异步电动机转子断条故障，占电动机故障的10%左右^[1]，对异步电机转子故障监测以便实施可靠诊断，有着重要的研究价值。常用的转子故障检测方法有多种，根据使用的信号不同有振动监测、电流监测、磁通监测、局部放电监测等^[2]。由于定子电流信号监测可做成非侵入式，因而有广泛的应用前景。异步电动机转子断条时，定子电流将出现特征频率分量(1±2ks)f0，(f0为基波频率，k为整数，s为转差率)，通过对定子电流频谱分析，可以实现故障的非接触检测。但电机稳态运行时，转差率很小，使得最强的故障分量频率(1±2ks)f0与基波频率很接近，且相对基波而言，故障分量幅度值较小，易被基波分量的泄漏及环境噪声所淹没，使检测的准确性降低，因此长期以来一直是电机故障检测的一个难点和热点。文献[3]提出了利用样条小波抵消工频信号分量影响，并取得了一定的效果，但使用小波进行频谱分析时的频率分辨率仍是一个待研究的课题。本文提出了一种基于Park矢量模平方函数的转子故障检测方法，将此方法结合高分辨率的MUSIC谱估计算法应用于电机转子断条故障检测，仿真及实验结果表明，取得了满意的结果。
2  基于Park矢量模平方函数的故障检测算法
    Park变换的基本思想是：将定子三相电流从(A,B,C )三维坐标转换到(D,Q)二维坐标，即

    当电机出现转子断条故障时，在电机定子电流谱中会产生频率为(1±2ks)f0的边瓣成分。其中k=1时的特征频率最强，在仅考虑k=1的条件下，主特征谐波频率为(1±2s)f0，此时电机定子电流的表达式如下

式中 Im为定子电流基频分量的最大值（A）；ω=2πf0为基波角频率；Il为电流低边瓣分量（(1-2s)f0）的最大值（A）；Ih为电流高边瓣分量（(1+2s)f0）的最大值（A）；α为基频分量的初始相角（rad）；β为低边瓣分量的初始相角(rad)；γ为高边瓣分量的初始相角(rad)。

    定义：电流Park矢量为I(t)，有I(t)=iD+jiQ，定子电流Park矢量的模平方函数为Is(t)。由式(6)、式(7)可得：

    由上式可知，在Is(t)的频谱中，仅含有直流分量、2sf0及4sf0特征频率分量，且频率间隔为2sf0，不含有基频分量，其最高频率分量4sf0比定子电流信号的最高频率成分(1+2s)f0低，在满足最低采样频率的条件下，其相对频率间隔增加，有利于频谱分析时频率分辨率的提高，因而可以提高特征频率检测的准确性。但用传统的FFT技术作频谱分析时的频率分辨率与采样数据长度密切相关，要获得较高的分辨率，应增加分析数据的长度，但其代价是噪声影响的增强和计算量的增大，因此，对短数据具有高分辨率，同时对噪声不灵敏的高分辨率频谱分析问题，一直成为频谱分析方法的 “瓶颈”。MUSIC（Multiple Signal Classification）方法[4]是一种基于数据自相关矩阵特征值分解的频率估计技术，它以有限个正弦函数和为信号模型，对短数据具有较高分辨率，同时又能抑制噪声的影响。因此本文采用MUSIC算法对Is(t)进行特征频率估计。假设输入数据为定子电流Park矢量的模平方函数Is(t)，它由L个正弦信号与白噪声组成，即

式中 d(n)为n时刻数据；e(n)是均值为0方差为σ2的复白噪声；Ak、fk及θk分别为第k个正弦谐波的幅度、频率和相位。

    理论上，当f=fk时，D(f)将在fk(1≤k≤L)处趋近于无穷大值，搜索D(f)的最大峰值点即可获得d(n)中的频率估计。由于MUSIC谱分析方法在低频段有较高的频率分辨率，且对噪声不敏感，应用于电流Park矢量模平方函数的特征谱估计，可准确检测电机转子断条故障。
3  计算机仿真研究
    设iA、iB、iC为异步电动机三相定子电流信号，分别为正弦信号、故障信号及噪声的叠加，基频f0=50Hz，电机在稳态运转时转差率s=2.33%,采样频率fs=1kHz，取△t=0.2s，采样数据长度N=200，进行仿真研究分析，其仿真结果如图1、图2所示。
    图1为应用上述算法的仿真结果，可以看出，采用该方法，可准确检测到转子断条时在定子电流中所产生的特征频率成分（2.3Hz，4.6Hz）。图2为应用传统的FFT技术的频谱分析结果。信号的频率分辨率而边瓣频率(1+2s)f0与电流信号的基频f0之间的频率间距△f=2.3Hz，因此无法分辨出特征频率成分；图2清楚的显示出基频成分（f0=50Hz），但无法分辨出边瓣成分（47.7Hz，52.3Hz），因此应用FFT分析技术，很难在短数据的情况下将故障特征频率成分检测出来。由仿真结果可知，采用本文提出的基于Park矢量模平方函数的高分辨率谱分析方法，减弱了定子电流基频信号的影响，可准确检测到定子电流信号中的特征频率分量，有利于转子断条故障的实时准确检测。

4  实验及结果
4.1  转子断条故障检测系统
    为了验证上述转子断条故障检测算法的有效性，实验中采用如图3所示的故障检测方案。电机选用Y132M-4型异步电动机，电动机带动交流发电机及电阻负载，在转子断裂1根导条的情况下进行试验，实验时低通滤波器通带截止频率fp为100Hz，A/D数据采集频率fs为1kHz。

4.2  实验结果及分析
    根据上述实验条件，在轻负载情况下，录取电机定子三相电流波形，取△t=0.2s的采样数据，应用测速计测得电机转速为np=1464r/min，电机稳态运行时转差率为

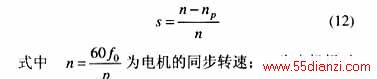
数，根据所选电机，p=2；实测电流信号基频f0=50.1Hz；据式(12)，可计算得s=0.024。应用上述故障检测算法，结果如图4所示。

[1] [2]  下一页