随着单台光伏逆变器技术的曰趋成熟和光伏发电规模的日益扩大,逆变器集群特性和控制逐渐受到重视。通过理论推导和实验验证,研究、探讨了并联逆变器集群的效率特性,得出使逆变系统总体效率最高的功率分配方式,这一成果将为逆变器集群控制策略的设计提供重要参考。
1 引言
随着单台逆变器技术的日趋成熟和光伏发电规模的日益扩大,逆变器集群特性和控制逐渐受到重视。文献指出逆变器共直流母线并联结构有助于提高逆变系统能效并降低发电成本。文献描述了一种群组概念:当光照较弱时,将各光伏电池组串并联,根据功率大小起动相应数量的逆变器,以求小功率时达到良好的输出电流质量和系统效率;当光照较强时,以多组串方式运行,每台变换器带一个组串,以实现更好的最大功率点跟踪。文献提出一种模块化光伏系统,任意时刻仅有一个模块工作在非满载状态,其余模块处于满载或待机状态。然而,共用直流母线的逆变器并联运行时,采取顺序投入方式好还是均流方式更好,需进一步明确。这里将对此问题进行探讨。
2 并联逆变器效率问题
对于如图1所示的共直流母线并联逆变器集群,可以通过合理投入逆变器数量和分配功率实现优化运行。
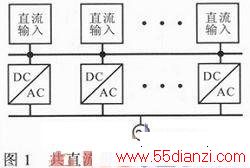
假设并联逆变器集群中,每台逆变器的效率不受其他逆变器的影响,在任何工作方式下仍保持各自原有效率特性,并且逆变器效率特性不随时间变化,则集群效率最优化问题可描述为:在给定总输入功率条件下,求各逆变器功率,使逆变系统输出总功率最大,即:
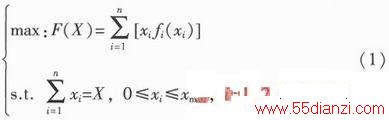
式中:i为逆变器序号;xi为逆变器i的输入功率;fi(xi)为输入功率为xi时,逆变器i的效率;X为总输入功率;xmaxi为逆变器i的最大输入功率;n为逆变器总数。
此优化问题可分为两步求解:①给定总功率和投入逆变器数量,求各逆变器功率分配,使总效率最高;②在上一步基础上,确定使总效率最高的逆变器投入数量。这里将从理论和实验两方面对以上第一步所述问题进行研究和探讨,并针对一种简化的情况推导以上第二步所述问题的解。
3 单台逆变器的效率模型
典型的单台逆变器效率特性曲线如图2所示。逆变效率η随功率P不同而非线性变化。在P较低区域,η严重下降,而在P中高区域,η较高。

对单台逆变器效率特性建模。将逆变器损耗分为4类:①电阻性损耗,即与电流平方成正比的损耗,例如线路和滤波电抗器内阻上的损耗、开关管通态损耗等;②与电压电流之积成正比的损耗,例如开关管开关损耗;③与电压平方成正比的损耗,例如均压电阻损耗、采样电阻损耗;④固定损耗,例如控制系统功耗。
当直流电压和电网电压不变时,上述损耗可合并为以下3类:与电流平方成正比的损耗、与电流成正比的损耗和固定损耗。设输入功率为x,输出功率为)y,有:y=x-(ay2+by+c),则:x=ay2+(b+1)y+c,设b’=b+1,于是得逆变效率η与y关系为:
![]()
考虑同一产品系列中不同功率等级的逆变器。设有一台基准逆变器最大输出功率为ymax,其效率特性满足式(2)。由于在同样技术条件下制造的不同逆变器效率特性相差较小,此处假设所有逆变器的效率特性曲线与基准逆变器的效率特性曲线形状相同,即,对于逆变器i,若其最大输出功率ymax=kiymax,则其效率特性为:
![]()
4 并联逆变器的效率特性
在单机效率模型基础上,研究共直流母线多机并联系统的效率。将并联逆变器系统效率最优化问题描述为:当总输出功率Y一定时,求各逆变器的输出功率yi,使总输入功率最小,即:

也就是说,各逆变器按照额定容量的比例分担Y时,系统有最高效率。将yi=λki代入式(3),可知此时各逆变器的效率相同,所以相应地直流侧按最大输入功率的比例分担功率。其特例是,当采用同型号的逆变器时,各逆变器功率均分可使总体效率最高。
下面讨论在给定总功率条件下,如何确定使总效率最高的逆变器投入台数。文献指出,可穷举所有可能的逆变器组合方式,分别求得各组合方式的效率特性,当给定总功率时,选取使总效率最高的组合。例如,4台逆变器并联运行,其中型号I(100 kW)共2台,型号II(250 kW)和型号III(500 kW)各1台,总功率950 kW,效率特性计算结果如图3所示。
图3a为各种逆变器组合的效率曲线,以及系统最优效率曲线。图3b示出为获得系统最佳效率ηbest,各种逆变器需投入的数量。可见,在系统总功率较小时,通过减少逆变器投入数量,共用直流母线的并联逆变器集群仍可达到较高的逆变效率。

对于同型号逆变器构成的集群,根据前文假设和分析,设单台逆变器效率满足式(3),则n台并联时的效率特性为:

5 实验验证
搭建实验平台对上述分析进行验证。两台10 kW三相并网光伏逆变器共直流母线并联,以光伏模拟器作为直流输入电源,输出为400 V三相电网。首先,测试单台逆变器的效率特性曲线;然后,测试两台逆变器功率均分时效率特性曲线;最后,测试两台逆变器功率不均分时的效率,并与功率均分时的效率进行对比。
单台逆变器效率特性如图4a所示。为验证此处所述的单台逆变器效率模型,取10组实测数据进行拟合。表1取其中5组实测值与拟合值对比。可见,拟合值与实测值十分接近,拟合优度判定系数R2=0.999 6,可知所提效率模型较为合理。
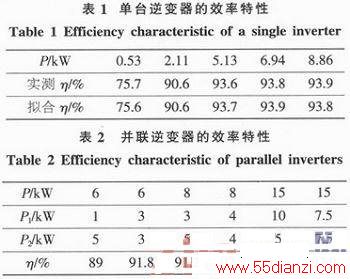
单台逆变器和两台并联逆变器的效率特性曲线如图4b所示。由图可见,当两台并联逆变器功率均分时,其总体效率曲线与单台逆变器效率曲线横轴放大一倍时基本一致。在同样的总功率下,两台逆变器功率均分时的效率高于功率不均分时的效率,具体数值对比见表2。
6 结论
此处建立并验证了单台光伏逆变器和共直流母线并联光伏逆变器的效率模型,推导了使并联逆变器总效率最高的功率分配方式,测试了并联逆变器在不同工况下的效率。理论和实验表明,若各逆变器效率特性相同,则当总功率和并联数一定时,按各逆变器最大功率的比例分担功率,可使总效率最高。其特例是,当采用同型号逆变器时,各逆变器功率均分可使总体效率最高。
本文关键字:逆变器 不间断电源-逆变器技术,电源动力技术 - 不间断电源-逆变器技术