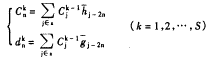（6）
式中，S为分解的层数，｛hi｝与｛gi｝为已设计好的小波滤波器。
Mallat快速分解法首先将数据f（n）分解为C1n与d1n，其中C1n为低频信号，d1n为高频信号。假设f（n）对应的频率ω满足｜ω｜＜Ω，则C1n所对应的频率满足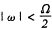
，d1n所对应的频率满足
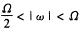。第二层分解是将C1n进行再分解。如此重复，则f（n）被分解成频率不同的成份：d1n，d2n，…，dsn，Csn。根据信号与噪声的频率特性，可以较容易地从这些频率不同的成份中区分出信号与噪声，从而完成信噪分离。
4．无衍射光束三角测量系统测量误差的小波处理
理想的贝塞尔光束信号是一曲线光滑、幅值变动较大的低频信号；而噪声的幅值变动较小，且呈不规则的随机状态，变动频率也较高，即噪声误差是高频信号。由于信号与噪声的频率特性不同，所以采用小波分析方法能将信号与噪声分离，进而剔除噪声误差。
图3所示是一模拟的理想贝塞尔光束信号，将它与图5所示的服从均匀分布的随机噪声相叠加，即得到存在噪声干扰的模拟信号，如图4所示。选用 Daubechies正交小波滤波器，根据式(6)对图4的信号数据进行三次小波分解，即可理想地分离信号与噪声，如图6和图7所示。通过多次理想光束加噪模拟试验，结果表明，经小波处理后，加噪光束峰值最大偏差由6μm减小到1μm，降噪效果显著。
如图8所示，CCD实测贝塞尔光束中含有噪声误差，中心光斑处出现多峰和峰值偏移，严重影响峰值的位置确定精度。
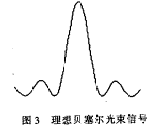
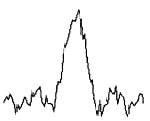
图4 理想光束信号+随机噪声
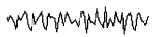
图5 服从均匀分布的随机噪声
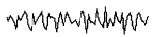
图6 小波分离的噪声
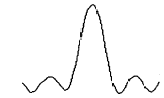
图7 去噪后的贝塞尔光束信号
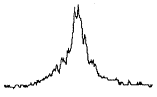
图8 CCD实测贝塞尔光束
图9所示为经小波处理后的实测贝塞尔光束。由图可见，经小波处理后，光束峰值位置突出、居中。经多次实测结果可知，实测信号峰值的最大偏差由3个像元减小到1个像元，使相应的位置测量精度显著提高。
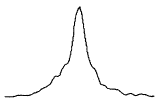
图9 经小波处理后的实测贝塞尔光束
