sin(n2π
)=0(7)
可见,串联后输出电压中基频成分为线性叠加。
当n=m时,有
cos(n2π
)=m,
sin(n2π
)=0(8)
可见,串联后输出电压中频率f=mfs的成分线性叠加。
因此,我们可以得知,m个输出依次时延Ts/m的SPWM逆变器串联,其输出的基频成分幅值为线性叠加,输出含有f=amfs(a=1,2,...)的谐波,谐波的幅值亦为线性叠加。
因此,若多重逆变器由m个单体逆变器组成,逆变器载波频率为fs,则第i个单体逆变器的时延为:
t=(9)
可见,通过串联叠加,输出频谱中所含谐波成分更加高频化,可大大减小滤波电感的体积。
3 仿真与实验
3.1 基于MATLAB的仿真实验
采用MATLAB对两个时延为Ts/2的单相SPWM叠加得到双重SPWM波的情况进行仿真,条件为:开关频率fs=2.5kHz,调制比为0.8,时延Ts/2。频域分析结果如图5所示。
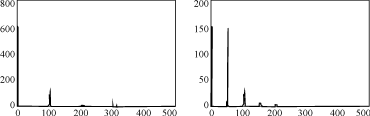
(a) 双重叠加输出电压的频谱分布 (b) 单个逆变器输出电压的频谱分布
图5 不同方式下输出电压的频谱分布
可见叠加后的波形中开关谐波频率增加1倍,基频和谐波成份都得到叠加,证实了以上分析结果。
3.2 电路实验
采用CM15-12H型的IGBT建立带高频输出变压器的单体全桥逆变器,逆变器为二重串联叠加结构,带小型滤波电感。控制方式采用相移PWM控制,采用ADSP2181为数字控制器,输出两路相互有时延的SPWM控制信号。输入电源由4节12V蓄电池串联提供,输出为220V,50Hz交流。
当开关频率为12kHz,时延为τ=42μs,负载为纯阻性,滤波输出波形如图6所示。波形的THD<3%。
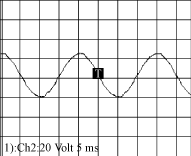
图6 实验的输出波形
4 结语
本文对相移PWM的输出频谱进行了分析,得出了时延与输出频谱之间的关系。仿真与实验的结果证实了分析的正确性。