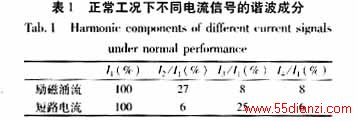
式(7)中j分别取2、3,得k1=(E(3)-E(2))/(3-2),反映了电流中所含2次谐波与3、4次谐波的能量变化;k2=(E(4)-E(3))/(4-3),反映了电流中所含基波与2次谐波的能量变化。判据k=k1/k2=( E(3)-E(2)) /((E(4)-E(3)),反映了电流信号中前四次谐波在不同尺度高频段上的能量变化情况。由于励磁涌流中2次谐波的含量大于其3、4次谐波,故图3中其ab段斜率k1为正;而铁芯饱和时,短路电流的能量谱图中a′b′段斜率k1为负。计算结果如表2所示,通过判据k的符号即可区分铁芯饱和状态下内部短路电流和励磁涌流。
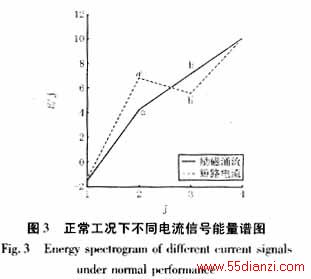
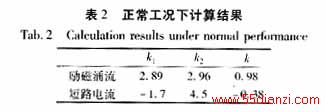
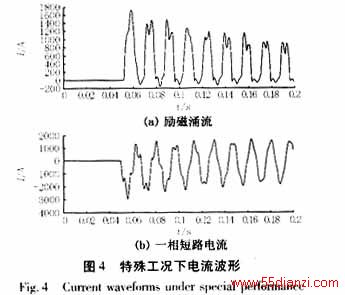
在某些特殊工况下,如有长线路串补电容的高压系统及有高压电缆的变压器,其励磁涌流和短路电流波形会发生畸变(图4),其中短路电流中二次谐波的含量会增大,如表3所示。
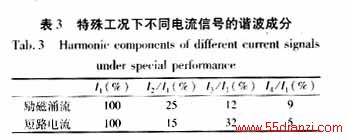
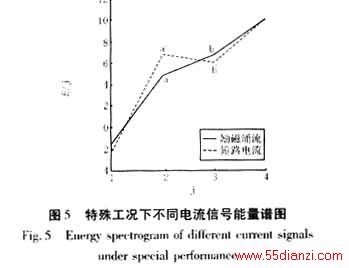
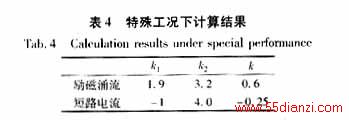
从图5中可以看出,在铁芯饱和状态下,即使短路电流的二次谐波的含量高达15%,由于其三次谐波的含量很大,a′b′段斜率k1仍为负。从计算结果表4中可知,本判据依然有效(仍可通过k的符号区分铁芯饱和状态下内部短路电流和励磁涌流。)在实际运用中,设定k的阈值,可以区分励磁涌流和短路电流(铁芯饱和状态下),从而在一定程度上有效的解决了在特殊工况下,因短路电流中二次谐波增大,导致变压器差动保护误判的问题。
5 结论
(1)本文基于小波多分辨率理论和小波能量谱,提出一种将能量变化率的比值作为判据,来区分变压器内部短路电流和励磁涌流的新方法—小波能量谱图解法。
(2)本判据同时考虑了内部短路电流和励磁涌流的前四次谐波,包含信息量丰富,形式简单,应用简便。
(3)在变压器铁芯饱和状态下,本判据区分内部短路电流和励磁涌流,十分有效,通过其符号即可区分。
(4)某些情况下,励磁涌流的二次谐波含量比例较小(有时可能是10%左右),但在所有的高次谐波中其含量比例仍是最大,此时该判据依然有效,从而避免了如何选取适当二次谐波制动比的难题。
(5)大量仿真表明:在信号的多分辨分析中,不同小波函数的选取,对结果会产生很大影响。本文选用的是db18小波函数。
本文关键字:变压器 电工文摘,电工技术 - 电工文摘