电力系统接地网故障诊断
张晓玲 黄青阳
(福州大学福州350002)(泉州电业局泉州362000)
摘 要 本文对电力系统发、变电站接地网故障诊断进行了研究，应用电网络理论和矩阵理论建立故障诊断方程，将能量最低原理、优化技术等有效地应用于接地网故障诊断，结合多激励法，从而有效地解决了欠定方程的求解问题；同时通过算例分析验证了该方法的正确性、可行性及实用性；讨论了可及节点数量变化对诊断结果的影响。
关键词 接地网 优化技术 故障诊断 多激励法
1引言
电力系统的接地网是维护电力系统安全可靠运行、保障运行人员和电气设备安全的重要措施，但往往由于接地网的均压导体的腐蚀、断裂或者漏焊等故障，引起或扩大事故，带来巨大的经济损失和不良的社会影响。
由故障诊断学理论可知,无论采用哪种方法建立起来的故障诊断方程均是欠定方程或病态方程。对于电力系统的接地网，由于其可及节点是有限的,建立的故障诊断方程无疑也是欠定方程，欠定方程的求解问题一直是故障诊断学里讨论的问题，并没有最终得到解决。因此，本文结合电网理论、矩阵理论、优化技术、能量学原理及多激励法对接地网的故障诊断问题进行讨论。
2故障诊断方程的建立
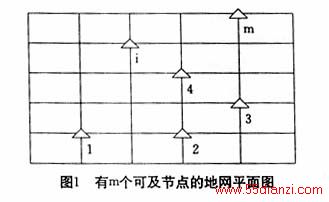
地网的平面结构如图1所示，设有n个独立节点，b条支路，m个可及节点。忽略电感和电容的影响，可以将地网等效为纯电阻性线性网络N，如图2所示。
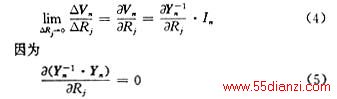
2.1灵敏度矩阵的求解
由电网络理论的节点分析法可得：
其中，A为节点关联矩阵，In为节点的电流源激励列向量(非激励接点的电流值为0)，Yb是支路导纳矩阵(该矩阵是对角阵，对角元素为Rj的倒数，其余元素为0，Rj是地网均压导体的支路电阻值，对于实际地网，可以根据地网的平面施工图计算得到），Vn为节点电压列向量，Yn是节点导纳矩阵。
由上面三个关系式可以推得单个支路电阻的变化对节点电压的影响，即对(3)式求Rj的偏导数，得
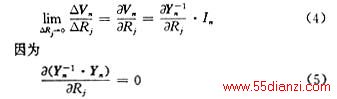
由(5)式可得
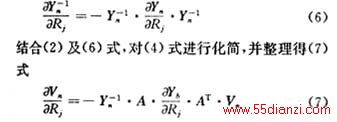
当给定地网的设计值或标称值，可通过（7）式计算每一条支路电阻变化时每个节点电压的变化量，方程右端的Vn代表节点电压的理论计算值或标称值，由(3)式求得。
由于Yb为对角矩阵，其对角元素为Rj的倒数，其余均为0，则
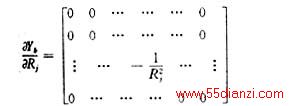
于是可得每一条支路电阻(Rj)变化时对节点电压Vn的影响，如果用0.01Rj乘上述矩阵的每一项，可得到Rj变化1%时对节点电压Vn的影响。
由上述方法求得的矩阵Vnb为n×b维矩阵，从中取出与m个可及节点有关的行向量，组成一个新的矩阵Vmb，并称此矩阵为灵敏度矩阵，其中各元素Vij代表的物理意义为当对可及节点施加激励时，第j个支路电阻的变化，对测量节点i电压的影响值；而传统的灵敏度矩阵是通过测量可及节点间的电阻建立的，由于此电阻值较小，因此对仪器仪表的精度要求较高，同时测量误差的影响也较大。
2.2故障诊断方程的确定
采用故障诊断学里的参数识别法［2］建立故障诊断方程，其故障参量为每段导体电阻增量的百分比。如果令Zn=
,Zmn是Zn中取出的与m个可及节点有关的行向量组成的阻抗矩阵，令m个可及节点电压列向量的理论计算值为Vm，测量值为
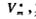其增量为ΔVm，于是有
由式(9)与灵敏度矩阵Vmb可建立故障诊断方程:
其中X是b维列向量，Xj代表第j段导体电阻增加倍数，由于它是一个相对量，故可以直接用于故障诊断。
3故障诊断方程的求解
当电流通过接地网的接地引线流入大地时,其电流是按恒定电流场原理进行分布的,但是仍然满足能量最低原理,如果施加直流源(由于电感和电容不消耗能量,交流源也适用),可以忽略电感及电容的影响,且地网中的主要能量损耗是由均压导体的发热引起。
假设地网中每段导体的实际电阻为:
=Rj0·(1+Xj)整个地网能量损耗表达式为：由于能量损耗最小，即是求P的极小值Pmin。
将以上整个推导过程中的矩阵形式，写成其分量表达式，则故障求解式由约束条件和目标函数两部分组成，而其中的约束条件由故障诊断方程的等式约束和电阻增量的非负约束所组成，即(12)和(13)式所组成的表达式。
如果故障前、后地网各段支路的电流相等，即Ij=Ij0,则上述的目标函数式(13)可以进一步化简为对P1求最小值，P1如(14)式所示。
于是由(12)和(14)两式构成的故障求解式是由线性目标函数与约束条件构成的数学模型，该模型是典型的优化技术中的线性规划问题，对其求解采用较成熟的线性规划理论中的单纯形法：通常采用两阶段法或大M法来寻找一个起始的基础可行解，然后采用非负减少规则来检验它的最优性；只要Vmb是非奇异矩阵，上述故障诊断方程就有唯一解。下面通过算例分析来验证该方法的正确性
4算例分析
对如图3所示地网结构进行仿真计算，均压导体采用非均匀分布形式，y方向导体的间隔距离分别为8 m、13 m、13 m、8 m，x方向导体的间隔距离为7.5 m、12.5 m、12.5 m、7.5 m，取钢材的截面积为0.707×10-3m2，电阻率为0.325×10-6Ω/m。利用欧姆定理可以计算出该地网各段导体的标称电阻值，仿真计算用5 Ω~0.008 Ω的电阻来模拟地网各段导体的断裂及不同程度的腐蚀情况(理论上支路断裂时，其电阻增加倍数为无穷大，但一般认为阻值增量大于5倍，就可判为断裂)。本文故障诊断的阈值取1.0，即认为腐蚀50%以上(电阻增加倍数大于1.0)判为支路断裂，相反，则判为腐蚀(此判据并非一固定值，可以根据具体情况进行设置)。
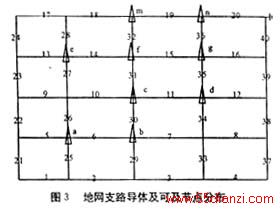
由于故障诊断方程为欠定方程，所求得的解是最优解，而不是实际解；故下表中的数据并不代表电阻的实际增加倍数，但完全能对故障进行定位；采用多激励法排除伪故障，伪故障的产生通常由于欠定方程的求解、电磁场干扰、测量误差及边缘效应的原因引起，但其重复出现的概率较小。
现以地网出现多条支路断裂或腐蚀为例进行仿真计算，假设第15、26条支路为故障支路，通过接入不同阻值的电阻来模拟支路故障，其诊断结果如表1所示，表中数字代表支路数，括号里的数字代表该支路电阻的增加倍数，带“▲”的支路为故障支路。该方法同样适用于单支路或两条以上支路出现故障的情况。
若地网出现不同程度的普遍腐蚀，仿真计算结果如表2所示，从表中数据可以看出，诊断结果与施加激励的位置有关。
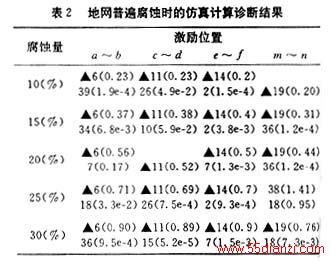
采用上述故障诊断方法，不论地网的均压导体是采用均匀分布还是非均匀分布，通过仿真计算，都能准确地诊断出地网的故障所在，包括地网的单条支路断裂、多条支路断裂、地网不同程度的腐蚀以及多种故障同时存在的情况。
5可及节点对诊断结果的影响
在工程实际中，可及节点的数量和位置不仅是有限的，而且是确定的，激励也只能加在现有的可及节点上，下面讨论可及节点数量的变化和施加激励位置不同对诊断结果的影响。
如图3所示的地网结构（共有24个独立节点，40条支路），假设第11条支路断裂和地网存在普遍腐蚀（腐蚀量为20%），可及节点数为10个，再依次减少可及节点数，然后改变施加激励的位置，其诊断结果如表3所示。
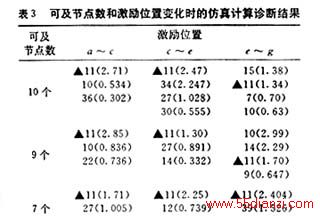
从上表中数据可以看出，故障诊断结果不受施加激励位置的限制，但可及节点数减少到一定值时(上例是减少到4)，出现故障诊断失真。因此，在现场测试中应尽量利用现有的可及节点，特别是重要设备附近的可及节点，有利于对故障的准确诊断。
6结论
(1)本文采用故障诊断中的参数识别法，直接利用故障参量(相对量)进行故障诊断，故该方法简单易行。
(2)本文利用电网络理论中的节点分析法，结合矩阵理论，推导出灵敏度矩阵，此矩阵直接反映了地网各段均压导体的电阻变化对可及节点测量电压的影响，该矩阵只受地网均压导体电阻热容量的影响，而导体电阻的热容量完全满足实际工程需要，从而避免了传统方法（通过测量可及节点间的电阻值）对仪器仪表精度要求较高的不足。
(3)采用多激励法有其显著的优越性，一方面可以有效地排除伪故障，另一方面，多激励法在分析和处理多次测量的诊断结果时，可以进行择优选择，故可以消除部分随机误差带来的干扰。
(4)本文将诊断理论、网络理论、矩阵理论及优化技术有机地结合起来，并有效地应用于电力系统发、变电站接地网的故障诊断中，从而有效地解决了欠定方程的求解问题，为地网无损伤检测提供了新的思路和方法，同时文中通过算例分析验证了该方法的正确性、可行性及实用性，故具有较高的理论和实用价值。
7参考文献
1姜建国，等.故障诊断学及其在电工中的应用.北京：科学出版社，1995.
2杨士元.模拟系统的故障诊断与可靠性设计.北京：清华大学出版社，1993.
3何献忠，等.优化技术及其应用.北京：北京理工大学出版社，1995.
本文关键字：暂无联系方式经验交流，电工技术 - 经验交流
