“圆心拟合法”测量短路故障情况下的动态频率
杨贵玉, 江道灼, 邱家驹
(浙江大学电气工程学院, 杭州 310027)
摘 要: 探讨短路情况下动态频率测量的一种新方法,提出的采用“圆心拟合法”对经过低通滤波的故障信号进行拟合处理,可以快速有效地从短路电流中分离出周期分量和非周期分量,进而精确计算出动态频率。该算法在对称或不对称短路故障情况下均适用,且启动时仅需三个连续的采样数据,具有时延小、精度高、稳定性好的优点。
关键词: 圆心拟合法; 动态频率; 短路故障; 同步发电机; 电力系统
Dynamic Frequency Measurement Under ShortCircuit Fault
by Using“Center Point Fitting”Method
YANG Guiyu, JIANG Daozhuo, QIU Jiaju
(Zhejiang University, Hangzhou 310027, China)
Abstract: "Center point fitting"-a new method of dynamic frequency tracking is presented.It can be used to decompose fundamental component and decaying DC component out from low pass filtered shortcircuit fault signals directly.Only last three sampling points are needed in each step.It is a realtime,high accurate and stable arithmetic on dynamic frequency measurement.
Key words: center point fitting; dynamic frequency; shortcircuit fault; synchronous machine; power system
1 概述
频率是衡量电能质量与系统稳定的重要指标。稳态情况下的系统频率基本稳定在(50±0.5) Hz范围内,对其准确跟踪测量的难度不大。但当系统发生严重短路故障时,频率可能发生较大幅度的振荡,且信号中存在较大的非周期分量和谐波分量,影响了频率的准确跟踪测量。
近年来,人们在动态测频理论和方法上进行了大量研究,并取得了很大的进展[1],尤其是提出了实时频率和等相角测量的概念[2,3],为动态精确测频提供了新的方法。目前已提出的几种典型的测频方法有虚拟转子法[4,5]、虚拟电势法[6]、频谱搬移法[7]以及小波分析法[8,9]等。除小波分析法外,其余3种方法都是基于电压信号正序分量频率的概念提出的,因而都采用三相电压信号的合成相量进行分析,测频的响应速度均为一个周期,因此属于一个周期内的平均频率(虚拟转子法 未给出测频的响应速度,这里不作比较)。小波分析法分析的是单相信号,其去噪声与分离非周期分量的效果令人满意,但是响应速度还不能满足实时跟踪的要求。
本文提出一种新的拟合算法——圆心拟合法。将三相短路电流信号合成为旋转相量,并对其旋转轨迹进行“圆心”拟合,进而求出并消除不同时刻的非周期分量,利用所获得的周期分量进行频率计算。该算法启动时仅需三个连续的采样数据,数据量小,实时性高,算法稳定。仿真结果表明有较好的拟合精度,可用于暂态信号分析和动态实时频率的测量。
2 三相电压合成相量的特点
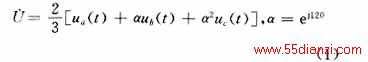
稳态运行情况下,发电机的电压是标准的正弦信号,三相之间互差120°,将三相电压按固 有的相量关系(1)进行迭加,可以得到一个瞬时合成电压相量,其实部与虚部即(α,β,0)坐标体系下的两个分量:Uα和Uβ。
系统电压幅值不发生变化时,合成相量的轨迹是一个圆,若不考虑谐波影响,无论频率是否 变化,轨迹曲线的曲率不变,且与零序分量无关。因此可以用相量的旋转角来测量实时频率,并运用“等相角采样”法提高测量的精度。
3 三相对称短路故障下的合成相量分析
系统发生短路时,会造成故障相的电压大幅度降低甚至消失。非对称短路情况下,测量装置 还可以采用非故障相的电压信号测频。但在三相短路情况下,装置可能无法取得电压信号。为确保故障情况下的信号数据真实性,装置可以暂时利用电流来测量频率[10],待电压恢复后再重新使用电压测频。由于短路残压、电流中都含有暂态分量,在靠近电源处短 路时尤为明显,而发电机短路电流有精确的数学模型,因此下面以发电机机端三相短路的电 流信号为基础推导“圆心拟合法”。
凸极同步发电机三相对称短路时A相电流表达式为

其它两相电流的初相角与A相电流互差120°,都含有一个衰减的直流分量,且短路初期暂态电流的幅值也在变化。式(2)中的2次谐波成分是因凸极机转子结构不对称所致,隐极机情况下可忽略不计。
按式(1)给出的方法将三相电流合成为瞬时电流相量,其轨迹如图1(a)所示,按基波频率确定的等相角采样点的分布情况如图1(b)所示(N=20点/周,图中仅绘出故障开始后3周)。由图1可以看出,直流分量和谐波分量对采样的影响比较严重,如果直接利用等相角采样法将导致很大的数值偏差。

4 圆心拟合法原理
由式(2)可知,短路电流中包含衰减直流分量、暂态及稳态周期分量等,其合成相量的轨 迹如图1(a)所示,其合成相量圆的圆心随直流分量的衰减而偏移,半径随暂态周期分 量的衰减而减小。圆心拟合法的目的是拟合出相量轨迹的圆心,即直流分量的衰减轨迹。
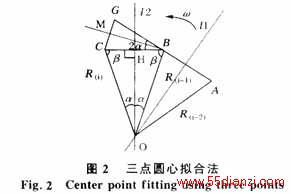
如图2所示,A、B、C为相继三个合成相量的位置,利用这三点可以拟合出一个圆,O为圆心。延长AB至G并取BG=AB,近似认为AB=BC,可以得到两个等腰相似三角形△GBC和△BOC,并有

式中:OB为ti-1时刻的拟合圆半径,以R(i-1)表示;β为OB与CB之间的夹角 。由式(3)并结合CB相角可以计算出拟合半径R(i-1)的幅值和相角,其相量算法如下
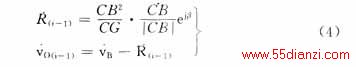
式中: O(i-1)为ti-1时刻的圆心偏移相量;
O(i-1)为ti-1时刻的圆心偏移相量; B为总合成 相量(图2中未绘出)。拟合得到的
B为总合成 相量(图2中未绘出)。拟合得到的 即为消除直流偏移的合成电流相量,圆心轨迹
即为消除直流偏移的合成电流相量,圆心轨迹 为直流分量的衰减轨迹。
为直流分量的衰减轨迹。
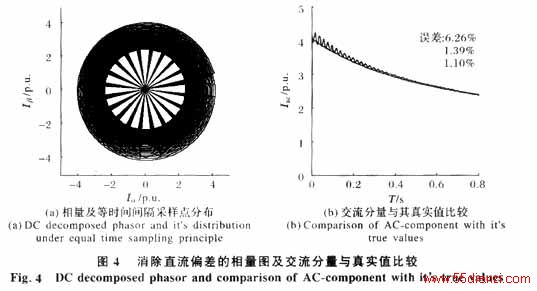
5 利用圆心拟合法消除直流分量
5.1不含二次谐波分量时的仿真结果
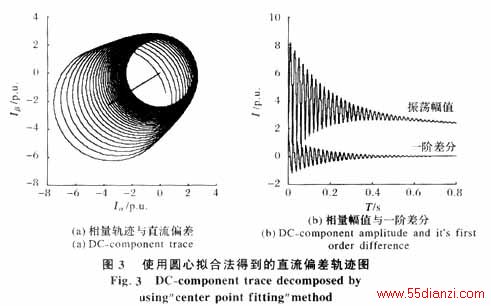
采用圆心拟合法对式(2)所示的电流信号进行仿真,其中,各参数值见表1。为考察拟合的准确程度,先取消式(2)中的二次分量,按隐极电机仿真,结果如图3~5所示。



图中|Emax|为最大绝对误差,按式(5)计算。
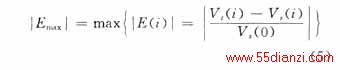
式中:Vs为实际值;Vt为拟合值;i为采样序号;0表示初值。|Eave|是指定仿真域内绝对误差|E(i)|的平均值;Eave是E(i)的平均值。图中误差顺序为  ,不再说明。
,不再说明。
由仿真结果可知,平均绝对误差|Eave|都在2.5%以下,Eave则更低,拟合的总体误差不大,拟合曲线与真实曲线基本吻合。
5.2 频率变化对拟合结果的影响
设短路时电机的频率按式(5)[3]规律变化:

动态频率情况下,圆心拟合法的拟合值与实际值的结果比较如图6、7所示。可见,圆心拟合法对频率变化不敏感,除了频率拟合偏差略有增大外,其它各量与固定频率下的仿真结果基本一样。因此,采用圆心拟合算法,跟踪测量动态频率是稳定的。


5.3 二次谐波分量对拟合结果的影响
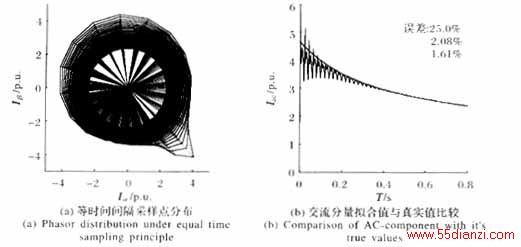
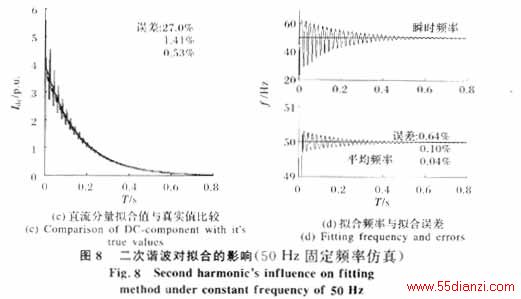
为估算谐波对拟合算法的影响,直接对式(2)所示短路电流进行全电流相量拟合仿真(其中二次谐波合成相量初值占基波合成相量初值的17.8%),结果如图8所示。
由图可知,谐波对频率拟合结果影响不大,但对其它拟合结果的影响较大,尤其是短路初期的拟合误差最大。比较图4(b)、图6(a)和图8(b)中交流分量的拟合误差可知,二次谐波对圆心拟合法的拟合误差有放大作用。
对含有随机干扰的信号仿真的结果表明,随机信号同样对拟合算法的精度产生不利影响(限于篇幅,略去有关仿真结果)。因此采用本文所述圆心拟合算法前,应预先对信号进行低通滤波处理,以消除高次谐波和随机干扰的不利影响。
6 圆心拟合法的误差分析
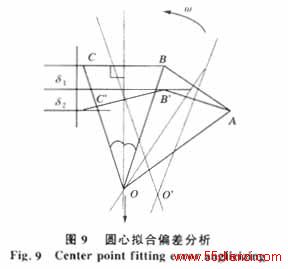
受衰减直流分量影响,合成相量轨迹的曲率会发生周期性变化,因而图3中三角形相似条件 将被破坏,使拟合相量圆与交流分量的相量圆的圆心位置存在偏差。如图9所示,因衰减直 流分量的影响,合成旋转相量的轨迹在t1、t2时刻从不考虑衰减影响时的B、C点分别下 移δ1、δ2到B′、C′点,由此拟合出的圆心位置则从O点偏移到O′点。直流 分量轨迹是指向原点的直线,合成相量圆心位置也应垂直向下偏移(图9中箭头方向)。可见,圆心拟合法不能精确恢复合成相量的圆心位置。另外,交流衰减分量也会对拟合产生不 良影响,而且各分量的衰减幅度越强烈,圆心拟合误差就越大,因此在拟合初期都存在较大 的误差,但随着衰减幅度减小,误差也相应降低。直流衰减分量及其它整倍次谐波分量对拟合的影响是周期性的,只要对测频结果每周作一次平均,就可有效抵消拟合引起的测频误差,如图5(b)、7、8(d)所示,经周波平均后的拟合频率,精度有很大提高。
7 不对称故障情况下的圆心拟合处理方法
系统发生不对称短路时,由于三相电压、电流之间的对称关系被破坏,合成相量的轨迹不是圆,因而不能直接使用拟合法。但是在相平面(s(t),ds(t)/dt)上,正弦信号与其一阶导数信号合成相量的轨迹仍然是一个旋转的圆,因此可以采用单相故障信号与其一阶差分进行合成,然后再利用拟合法。

式中:首项为直流衰减分量,它不影响暂态基波分量的合成;末项是二倍频以上的谐波分量,可对原信号S·(t)进行低通滤波加以消除;第2项即暂态基波分量,其初始值为A1(α1/ω1+j),从式(2)和表1所列参数值可以看出,α1/ω1值很小(不到1%),因此可以忽略不计。这样,暂态基波分量就可近似用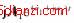 等效,并与原信号正交。令
等效,并与原信号正交。令

由式(7)所示的合成相量的旋转轨迹是一个圆,因此可以利用本文提出的圆心拟合法进行测频。不过,如果采样过程中运用了等相角采样,在做差分等效时还必须考虑动态采样周期的影响。
8 结论
1)“圆心拟合法”利用三个连续的采样数据进行三相短路故障信号的相量拟合处理,可以快速有效地从短路电流中分离出周期分量和非周期分量,进而计算出动态频率;在不对称短路故障情况下,只要对故障信号进行适当的合成处理,该方法同样有效。
2)该算法基本不受采样频率与系统频率的影响,且启动时仅需三个连续的采样数据,具有时延小、稳定性好的优点,平滑后的频率能满足工程需要。
3)拟合误差与采样频率之间关系不大,提高采样频率,只会使拟合轨迹更光滑,不会减小拟合误差。故文中仅以20点采样做仿真。
4)采用圆心拟合法时,输入的故障电流信号需经低通滤波处理,否则其测频精度将会受到高次谐波与随机干扰的影响,这也是各种测频方法必须面对的基本问题。
参考文献
[1]谢小荣,韩英铎.电力系统频率测量综述[J].电力系统自动化,1999,23 (3):54-57
[2]Moore P J,Allmeling J H,Johns A T.Frequency relaying based on inst antaneous frequency measurement[J].IEEE Trans on Power Delivery,1996,11(4):17 37-1742
[3]闵勇,丁仁杰,等.自适应调整采样率的相量在线测量算法研究[J].电力系统自动化,1998,22(10):10-13
[4]韩英铎,王仲鸿,等.电力系统动态频率的定义及“虚拟转子法”频率测量研究[J].清华大学学报(自然科学版),1993,33(1):1-9
[5]韩英铎,闵勇,等.电力系统动态频率的新概念和新算法[J].电力系统自动化,1993,17(10):5-9
[6]崔学深,郭志忠,等.电力系统动态频率测量的“虚拟电枢磁势”法[J]. 中国电力,2000,33(8):31-34
[7]王文举,贺益康,等.同步基准信号自适应滤波及在复杂供用电系统谐波检测中的应用[J].中国电机工程学报,2001,21(6):5-8
[8]Yang Hongtzer,Liao Chiungchou.A denoising scheme for enhancing waveletbased power quality monitoring system[J].IEEE Trans on Power Deliv ery,2001,16(3):353-360
[9]杨纪明,马志瀛,等.基于小波变换的短路电流各分量的计算[J].电工技术杂志,1999,11(6):13-15
[10]何奔腾,金华烽.电力系统震荡频率的实时估算[J].电力系统自动化,2000,24(15):17-20
[11]索南加乐,葛耀中,王安定,等.一种不受电压过零点影响的新型频率测量方法[J].电力系统及其自动化学报.1996,8(4):18-22
[12]张瑛,牟龙华,刘军.电力系统频率测量及跟踪[J].电力系统及其自动化学报,2003,15(3):35-36
本文关键字:测量 动态 经验交流,电工技术 - 经验交流
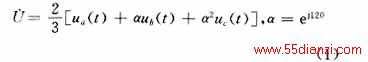



![]() O(i-1)为ti-1时刻的圆心偏移相量;
O(i-1)为ti-1时刻的圆心偏移相量;![]() B为总合成
B为总合成![]() 即为消除直流偏移的合成电流相
即为消除直流偏移的合成电流相![]() 为直流分量的衰减轨迹。
为直流分量的衰减轨迹。





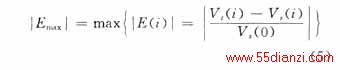
![]() ,不再说明。
,不再说明。






![]() 等效,并与原信号正交。令
等效,并与原信号正交。令