文章对高压电网中变电设备在真空注油或运行中,由于绝缘油的高速流动引起的流动带电现象进行了定量分析。通过讨论二维流动稳态均布电荷的计算方法、边界条件的确定,得出影响流动带电的相关因素及其影响程度,最后给出了建模变压器中绝缘油流动带电电流和极限电流的计算公式、各系数的确定方法及其近似计算公式。公式表明控制绝缘油的流速是避免变压器流动带电灾害的重要途径。
1 引言
电网中大量使用的变电设备仍以绝缘油作绝缘材料的居多,向变压器等电力设备进行真空注油及运行中冷却油泵运转时,由油流带电引起的变压器事故或故障时有发生,这已引起了各国电力部门的广泛关注,许多国家纷纷开展变压器油流带电的研究[1,2],特别是在高压、超高压大型变压器中,如何对绝缘油进行定量分析,计算绝缘油的流动带电量值,对避免灾害性事故的发生是非常有益的。
本文在国内外学者提出的流动作用机理和电动作用机理两种机理模型基础上,尤其是参考了美、日等国家研究人员的建模变压器原型[3,4],针对变压器绝缘油道的特点,给出了变压器流动带电的计算方法。本文的计算公式可供相关专业工程人员在分析、计算或研究中参考。
2 二维流动稳态均布电荷的计算
首先假设绝缘油是在一个2 L×W矩形管道内流过[5],即两个平行表面(导电的或绝缘的)之间的二维流动,如图1所示。则描述表面之间稳态电荷分布ρ(x, z)的方程应为
![]()
式中τ=εε0/σ为具有绝缘油电导率σ的流体中的特征削减电荷,D为扩散常数。

通常方程(1)难以对实际流体速度剖面图![]() 求解,但如果假设
求解,但如果假设![]() ,即
,即![]() 为一个均匀速度剖面图时,则可获得一个有用解。式中
为一个均匀速度剖面图时,则可获得一个有用解。式中![]() 是沿Z轴的单位矢量,均匀速度u是一个有效速度,它是这样定义的:使y方向上单位距离流体中的真正流动电流,即
是沿Z轴的单位矢量,均匀速度u是一个有效速度,它是这样定义的:使y方向上单位距离流体中的真正流动电流,即
![]()
式中ρ是电荷密度,当![]() 时,由式(1)的解给出。参数W是上述假设的矩形管道2L×W的宽度,并且假设W>>L。
时,由式(1)的解给出。参数W是上述假设的矩形管道2L×W的宽度,并且假设W>>L。
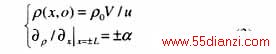
式中 V是管道中的平均流速。
式中Z为每个离子的单位电荷数;F为法拉第数;C0为离子浓度;n为迁移数;d为扩散层厚度;KA为油–壁界面的离子吸附率。
式中CA为表面上吸附点浓度;△F为由外部因素(例如施加一个外电场)引起的自由能变化;△F*为吸附过程的激活自由能。
3 变压器中的电流计算[4]
通过将式(7)插入式(2)并积分,得出在z=Z0处从管道出来的流动电流,其结果为
3.2 极限流动电流计算
如果将式(10)代入式(9),则极限流动电流可以表示成
这就是在建模变压器起电时采用的形式。
式中Nsc=v/D为施密特数;NRe=2rV/v为管子雷诺数。有效速度u取决于德拜长度和边界层厚度,这个依赖关系可用一个经验公式表达成
式中δ/δB为德拜长度与边界层厚度之比;m为约等于1的修正系数。
且对于W >> L的矩形管道,式(12)和(15)中的管子半径r可由L近似取代。
根据Gavis和Koszman的流动起电原理及Glasstone、Laidler和Eyring的电化学过程,系数α可写成(/-符号是由正/负流动电流决定的,即是由流体–管壁界面的负/正离子决定的)

按照绝对反应速率理论,表面KA的离子吸附率为
![]()
在得出方程(4)时,离子吸附的逆反应即离子从表面的逃逸现象,这里认为可以忽略。
由给出的边界条件方程A3和A4,可证明式(1)对ρ的解为
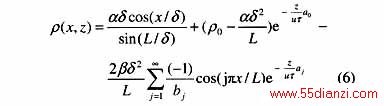
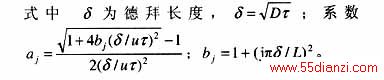
3.1 流动带电电流计算
当δ/(uτ)<<1时,就为实际变压器的实例,此时式(6)可近似表示为
![]()
![]()
根据式(8)预测对于Z0→∞时的极限流动电流为


为利用式(11)计算I∞,须确定有效速度u和扩散层厚度d。假设扩散厚度均匀,则管流可近似为

![]()
假设δB能用层流边界层近似描述,则对于管流有
![]()
4结论
影响变压器绝缘油流动带电的因素很多,在对变压器等高电压设备结构设计时应加以充分考虑,但对变电设备的使用人员而言,尤其是对中大型变压器进行真空注油时,最重要的是控制绝缘油的流速。控制油流速度可有效避免变压器故障或事故的发生,减少变压器油流带电引起的灾害。
本文关键字:暂无联系方式电力配电知识,电工技术 - 电力配电知识
上一篇:高压限流熔断器的选用