1 电阻炉炉温控制系统的硬件设计
电阻炉炉温控制系统采用上位机和下位机通信的控制方案。下位机采用以Intel8098单片机为核心的STD总线结构，充分利用了STD总线的高可靠性、高度模块化、标准化、成本低、使用方便等特点。下位机与上位机IBM-PC通过串行口RS-232进行联络，实现系统的调试和监控。通过PC机向下位机传送控制命令，而下位机将数据或结果传给PC机，由PC机完成绘图、打印等功能。系统的总体结构如图1所示。
2 动态矩阵预测控制算法
具体的动态矩阵控制算法参见文献[3～4]。
(1)输入柔化
为避免系统输入急剧变化，经过一个一阶惯性环节对期望跟踪值C(k)作柔化得到参考输入W(k)：
W(k)=[w(k),w(k＋1),…,w(k＋p－1)]T (1)
y(k)为k时刻系统输出，δ为柔化系数，p为预测步数。
(2)闭环预测
由于采用滚动优化方式，每次对系统仅施加第1个控制增量Δu(k)，因此其开环预测为
YM(k)=Yp0(k)＋αiΔu(k) (3)
式中 Yp0(k)为k前一时刻系统输出的p步预测，向量αi=[α1,α2,…，αp]T为模型向量。
闭环预测为开环预测加上反馈校正：
Yp(k)=YM(k)＋hi[Y(k＋1)－YM(k)] (4)
式中 hi为误差校正系数。
(3)滚动时域优化
在滚动优化时，取目标函数为如下形式的二次性能指标：
式中 Q、R为权阵，Q≥0，R>0。
在实施控制中，仅将Δu(k)施加于系统，令
dT=[1，0，…，0][ATQA＋R]-1ATQ=
[d1，d2，…，dp] (6)
式中 A为P×M维模型矩阵，M表示控制时域长度。
dT可离线设计，在线仅需计算点积：
Δu(k)=dT·[W(k)－Yp(k)] (7)
u(k)=u(k－1)＋Δu(k) (8)
3 参数设计
电阻炉系统是一个纯滞后大惯性环节，因此其参数整定与常规对象有所不同。这些参数的选择将直接影响到控制性能。
(1)采样周期T和建模时域长度N的选择 采样周期T的选择和建模时域长度N的选择密切相关，T越小，N越大，计算量也越大，但此时系统的抗干扰能力越强；反之亦然。
为了提高系统稳态时的抗干扰能力，我们取T=9s。因为纯滞后环节的存在，所以阶跃响应系数前几项为零。此系统采样周期较小而对象的过渡过程时间很长，但其阶跃响应经一段复杂的动态变化后呈指数上升形式。因此，N的选择不需延伸到阶跃响应的稳态，只要使N·T覆盖阶跃响应动态变化激烈的部分即可。这时，最后一个状态量的计算不能再用平推公式YN(k)=YN－1(k)，而应用递推公式：
YN(k)=（1＋σ)YN－1(k)－σYN－2(k) (9)
式中 σ=exp(－T/Ta)，Ta是阶跃响应后面部分的时间常数，它不用精确计算，σ可在线凑试。这相当于把模型截断后的指数上升信息都集中到参数σ中反映出来，实际上是前N－1个数据形成的阶跃模型和最后一步的参数化模型的组合。基于上述分析，经多次仿真计算，我们取N=50。利用飞升曲线，可得到其模型向量αi。
(2)控制时域长度M的选择 小的M值有利于控制系统的稳定，但对复杂系统来说，得到的动态性能太差。大的M值则表征允许有较多步的控制增量变化，从而增大控制的灵活性，有较快速的响应，但有可能引起不稳定。兼顾控制的快速性与稳定性，取M=3。
(3)最优化时域长度P P必须满足条件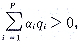
这样控制系统才有可能达到稳定，同时考虑到其对动态特性的影响，我们取P=20。
(4)误差权矩阵Q和控制权矩阵R 在最优化指标式(6)中，Q为一对角阵，权系数qi的选择决定了相应误差项在最优化指标中所占的比重。我们取Q=I，I为单位矩阵。为了压制控制增量的剧烈变化，取R为0.1I。
(5)误差校正矢量h 误差校正矢量h的选择不取决于其它设计参数，它仅在对象受到不可知扰动或存在模型误差使预测的输出值与实际输出值不一致时才起作用。取h1=1.0，hi=0.9，i=2，3，…，N。
4 仿真与实际运行结果
按照以上所设计的参数，我们进行了计算机仿真，仿真结果如图2所示。
将此算法应用于实际电阻炉中，收到了很好的效果，在工业控制现场所得的实际控制曲线如图3所示。在此之前系统采用的是传统PID控制，其仿真曲线及现场实际控制曲线分别如图4、5所示。将两者相比，可以看出，由于动态矩阵控制算法能不断地在线优化，从而使得系统适应性增强，响应速度加快，超调减小，调节时间缩短，稳定性加强，控制精度最终达到±1℃之内。
5 结束语
我们针对炉温控制系统这一纯滞后大惯性环节设计了动态矩阵预测控制器，并通过对阶跃响应系数的处理，有效地将动态矩阵控制算法应用于大惯性及纯滞后的工业对象，获得了良好的控制性能。该系统已在湖北汽车配件厂投入使用，现场运行结果表明，该系统控制精度高，稳定性及抗干扰能力强，有效地保证了钢件加热的温度，提高了产品的合格率，具有一定的实际应用价值。
参考文献
1 Vance J V. Advances in model-based control technology. Control Engineering, 1994,41(10):77～ 82
2 Richalet J, Raulat A. Model prediction heuristic control. Automatica, 1978, 14(2):413～ 428
3 席裕庚.预测控制.北京：国防工业出版社，1993.149～173
4 陈福祥.预测控制及应用.武汉：华中理工大学出版社，1993.82～97
本文关键字：动态 电子技术，电工技术 - 电子技术
上一篇：UPS短信报警控制方案
